Ejercicios

1.

El teorema de Euler afirma que para un número a y un número m , se tiene:

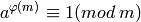
para la función 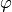de Euler, siempre que a y m sean primos entre sí.

• Escribe un programa que compruebe el teorema para los números m menores que 1000 y todos los números a<m.
• ¿Es cierto que si se verifica la igualdad, entonces necesariamente a y m son primos entre sí? Busca un contraejemplo, o verífica la propiedad para todos los números m menores que 1000.
• ¿Es siempre el menor número posible que verifica esta identidad para todos los números a que son primos relativos con m ? Busca un contraejemplo, o verífica la propiedad para todos los números m menores que 1000.
• Dados dos números a y m , encuentra el menor número positivo k tal que
• Dado un número m , encuentra el menor número positivo k tal que para todo a que sea primo relativo con m . Llamemos al número k así obtenido.

2.

Como vimos en el ejercicio anterior, 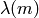no siempre coincide con 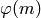. Para cada una de las preguntas siguientes, busca un contraejemplo, o verifica la propiedad para todos los números menores que 1000.

• ¿Coinciden siempre para los números cuando p es primo?
• ¿Coinciden siempre para los números cuando p es primo impar ?
• ¿Coinciden siempre para los números cuando p y q son primos impares?

3. Ejercicio opcional

• Intenta relacionar con los valores de y .
• Conjetura una fórmula que expresa en función de , ,... hasta .

4. Raíces racionales de polinomios con coeficientes enteros

Comprueba el criterio que aprendimos en secundaria sobre las raíces racionales de un polinomio con coeficientes enteros:

Cualquier raíz racional de un polinomio con coeficientes enteros tiene un numerador que divide al término independiente y un denominador que divide al coeficiente del término de mayor grado.

• Escribe código que busque las raíces de un polinomio con coeficientes enteros según este criterio
• Escribe código que compruebe que el resultado coincide con el resultado de llamar al método roots, para un conjunto de polinomios que te parezca lo bastante significativo.

5.

Investiga la siguiente pregunta:

Dado un polinomio p con coeficientes enteros, ¿para cuántos valores de k el polinomio p+k es reducible? ¿para cuántos valores tiene al menos una raíz (entera)?

• Escribe una función que acepte como argumentos un polinomio p con coeficientes enteros y dos enteros k1 y k2 , y devuelva en una lista todos los enteros j entre k1 y k2 tal que p+j tiene alguna raíz entera.
• Escribe una función que acepte como argumentos un polinomio p con coeficientes enteros y dos enteros k1 y k2 , y devuelva en una lista todos los enteros j entre k1 y k2 tal que p+j es reducible sobre .
• ¿Te parece razonable la siguiente conjetura?: “La cantidad de enteros j en el intervalo [-K, K] tal que p+j tiene alguna raíz entera crece como , donde n es el grado del polinomio p ”. Medita un momento al respecto.
• Argumenta con datos empíricos si la conjetura análoga para polinomios reducibles es razonable, o no, estimando el ratio entre los polinomios que verifican una u otra condición.