Sage tiene definidos un buen número de anillos, grupos y otras estructuras algebraicas.
Podemos operar con elementos que representan elementos de un anillo o un espacio vectorial, por ejemplo, además de con objetos que representan anillos, grupos, subgrupos, subespacios vectoriales y otras estructuras de nivel más alto.
Muchos anillos comunes están definidos en Sage:
- ZZ :
- Integers(m) :
(ó
)
- QQ :
- RR :
, representados por números reales de doble precisión
- CC :
, representados por números reales de doble precisión
Además, podemos usar otros constructores para definir anillos derivados, como el constructor de anillos de polinomios PolynomialRing que veremos en detalle más abajo.
sage: R1 = Integers(7)
sage: R2 = Integers(21)
sage: a = ZZ(3)
sage: b = R1(3)
sage: c = R2(3)
sage: print a, a.parent()
sage: print b, b.parent()
sage: print c, c.parent()
3 Integer Ring
3 Ring of integers modulo 7
3 Ring of integers modulo 21
sage: #Al calcular el inverso, Sage puede devolver el inverso
sage: #en el cuerpo de fracciones del anillo(en QQ en vez de ZZ)
sage: print a, 1/a, (1/a).parent()
sage: #Si el anillo es un cuerpo, obtenemos un elemento del mismo anillo
sage: print b, 1/b, (1/b).parent()
sage: #Si el anillo no es dominio de integridad, algunos elementos
sage: #no tienen inversos (en ningún cuerpo que contenga al anillo)
sage: print c, 1/c, (1/c).parent()
3 1/3 Rational Field
3 5 Ring of integers modulo 7
3
Traceback (most recent call last):
...
ZeroDivisionError: Inverse does not exist.
En el caso de 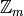 , podemos trabajar de forma más abstracta con elementos de Integers(m) ó bien a nivel más bajo usando números enteros normales, pero tomando restos módulo m. Estudiar los pasos necesarios en detalle es ilustrativo.
, podemos trabajar de forma más abstracta con elementos de Integers(m) ó bien a nivel más bajo usando números enteros normales, pero tomando restos módulo m. Estudiar los pasos necesarios en detalle es ilustrativo.
Para hacer sumas y productos sobre clases de equivalencia, podemos usar la suma y el producto habituales de números enteros, y tomar el resto de dividir por m :
m=31
a=12
b=23
s=(a+b)%m
p=(a*b)%m
Aunque podemos calcular la clase de congruencia de 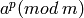 calculando el entero
calculando el entero 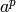 y luego tomando el resto módulo m , debemos tener en cuenta que
y luego tomando el resto módulo m , debemos tener en cuenta que 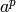 puede ser un número muy grande, y el ordenador puede dedicar al cálculo demasiado tiempo y memoria. En este caso, compensa reducir el número módulo m después de cada producto:
puede ser un número muy grande, y el ordenador puede dedicar al cálculo demasiado tiempo y memoria. En este caso, compensa reducir el número módulo m después de cada producto:
sage: def potencia1(x, n, m):
... if n == 0:
... return 1
... elif n%2 == 0:
... y = potencia1(x, n/2, m)
... return (y*y)%m
... else:
... y = potencia1(x, (n-1)/2, m)
... return (x*y*y)%m
sage: potencia1(3,8,10)
1
También podemos usar la función power_mod:
sage: power_mod(3,8,10)
1
El algoritmo correspondiente para Integers(m) es válido para cualquier anillo con unidad (el 1 que aparece en el código se transformará en la unidad del anillo).
sage: def potencia(x, n):
... if n == 0:
... return 1
... elif n%2 == 0:
... y = potencia(x, n/2)
... return y*y
... else:
... y = potencia(x, (n-1)/2)
... return x*y*y
sage: a = ZZ(3)
sage: b = R1(3)
sage: c = R2(3)
sage: print potencia(a, 8)
sage: print potencia(b, 8)
sage: print potencia(c, 8)
6561
2
9
El inverso de a módulo m, es decir, la clase b tal que 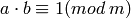 , no se puede reducir a una operación de aritmética usual. Una llamada a la función inverse_mod(a,m) devuelve el inverso de a módulo m (este número se calcula usando los coeficientes de una identidad de Bézout). La operación equivalente en Integers(m) es 1/a .
, no se puede reducir a una operación de aritmética usual. Una llamada a la función inverse_mod(a,m) devuelve el inverso de a módulo m (este número se calcula usando los coeficientes de una identidad de Bézout). La operación equivalente en Integers(m) es 1/a .
sage: inverse_mod(3,7)
5
sage: R1 = Integers(7)
sage: b = R1(3)
sage: 1/b
5
La sintaxis para definir un anillo de polinomios con coeficientes en otro anillo R es:
Pols.<t> = PolynomialRing(R)
ó
Pols.<t> = R['t']
donde hemos definido el anillo de polinomios Pols con coeficientes en el anillo R y la variable independiente t .
sage: #Definimos varios anillos de polinomios con coeficientes en distintos anillos
sage: PR1.<t> = PolynomialRing(ZZ)
sage: PR2.<x> = PolynomialRing(QQ)
sage: PR3.<y> = PolynomialRing(RR)
sage: PR4.<z> = PolynomialRing(CC)
sage: R1 = Integers(7)
sage: PR5.<u> = PolynomialRing(R1)
Una vez hemos definido el anillo, podemos usar la variable independiente para definir polinomios, operando con ella como una variable más.
sage: p=t^2-1
sage: q=x^2-1
sage: p.base_ring()
Integer Ring
sage: q.base_ring()
Rational Field
La variable p tiene tipo de datos “Polinomio con coeficientes enteros”.
La variable q tiene tipo de datos “Polinomio con coeficientes racionales”.
sage: p?
<html>...</html>
sage: q?
<html>...</html>
Podemos evaluar un polinomio en un punto con la sintaxis
p(var=expresion)
donde var es la variable independiente del polinomio y expresion es cualquier expresión en SAGE que dé como resultado un elemento del anillo.
sage: print p(t=2)
sage: print q(x=1+2)
sage: numero=0
sage: print q(x=numero)
sage: print [q(x=j) for j in range(-3,4)]
3
8
-1
[8, 3, 0, -1, 0, 3, 8]
Para dibujar la gráfica de un polinomio usamos el comando plot .
sage: #Dibuja el polinomio entre -2 y 2
sage: q.plot(-2,2)
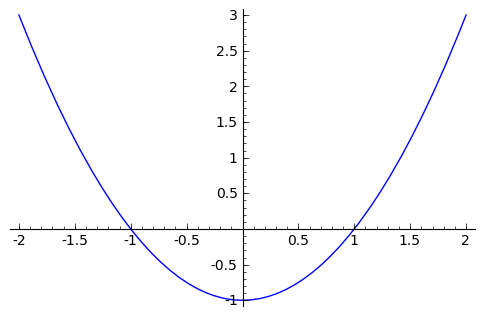
Una raíz de un polinomio ![p\in R[t]](_images/math/cb4924bb8099f7417a2eff6636d0eb7a79d11e39.png) es un elemento x0 del anillo R tal que p(x0)=0 . El teorema fundamental del álgebra afirma que un polinomio de grado n con coeficientes complejos tiene exactamente n raíces complejas. Sin embargo, un polinomio con coeficientes enteros puede tener raíces que son números racionales, reales algebraicos, o complejos.
es un elemento x0 del anillo R tal que p(x0)=0 . El teorema fundamental del álgebra afirma que un polinomio de grado n con coeficientes complejos tiene exactamente n raíces complejas. Sin embargo, un polinomio con coeficientes enteros puede tener raíces que son números racionales, reales algebraicos, o complejos.
El método roots se puede llamar desde cualquier polinomio, y devuelve una lista de tuplas que contienen las raíces del polinomio con sus multiplicidades. Atención, si las raíces de un polinomio no están en el anillo de sus coeficientes, el método roots no las devuelve, y tenemos que llamar a real_roots o complex_roots .
sage: p.roots()
[(1, 1), (-1, 1)]
sage: p2=x^2-2
sage: p2.roots()
[]
sage: p2.real_roots()
[-1.41421356237310, 1.41421356237310]
sage: p3=x^2+1
sage: p3.roots()
[]
sage: p3.real_roots()
[]
sage: p3.complex_roots()
[-1.00000000000000*I, 1.00000000000000*I]
sage: r=z^2+1
sage: r.roots()
[(-1.00000000000000*I, 1), (1.00000000000000*I, 1)]
El método roots devuelve sólo las raíces enteras, y real_roots devuelve todas las raíces reales, y además lo hace de forma numérica. Sin embargo, SAGE tiene una alternativa a nuestro método raices: extender el polinomio a un polinomio con coeficientes racionales, y entonces el método roots devuelve las raíces racionales.
sage: s1 = 2*t-1
sage: print s1.roots()
[]
sage: qs1 = s1.base_extend(QQ)
sage: print qs1.roots()
[(1/2, 1)]
sage: s1.real_roots()
[0.500000000000000]
En un anillo como ![\mathbb{Z}_m[u]](_images/math/8ece17078176b6838ed7a2aacb5296de529df11b.png) , se aplica la misma definición de raíz del polinomio.
, se aplica la misma definición de raíz del polinomio.
sage: r = u^2+3
sage: r.roots()
[(5, 1), (2, 1)]
sage: #evaluamos r en todos los elementos de Z_7
sage: print [(j, r(u=j)) for j in srange(7)]
[(0, 3), (1, 4), (2, 0), (3, 5), (4, 5), (5, 0), (6, 4)]
Si un polinomio con coeficientes en 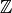 ,
, 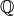 ó
ó 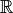 no tiene tantas raíces (contando multiplicidades) como su grado, no se puede escribir como producto de factores lineales. Aun así, se puede escribir como producto de factores irreducibles (es decir, factores que no se pueden expresar como producto de polinomios de menor grado):
no tiene tantas raíces (contando multiplicidades) como su grado, no se puede escribir como producto de factores lineales. Aun así, se puede escribir como producto de factores irreducibles (es decir, factores que no se pueden expresar como producto de polinomios de menor grado):
- factor(q) ó q.factor() : la factorización del polinomio
- list(q.factor()) : lista de tuplas (factor, multiplicidad)
- q.is_irreducible() : True si y sólo si q es irreducible.
sage: q=t^3 - 3*t^2 + 4
sage: print q.factor()
sage: print list(q.factor())
(t + 1) * (t - 2)^2
[(t + 1, 1), (t - 2, 2)]
sage: print q, q.is_irreducible()
sage: print q+1, (q+1).is_irreducible()
t^3 - 3*t^2 + 4 False
t^3 - 3*t^2 + 5 True
list(polinomio)
devuelve una lista con los coeficientes de polinomio , ordenados de menor a mayor grado.
sage: s1=2*z^2-3*z+1
sage: print s1
2.00000000000000*z^2 - 3.00000000000000*z + 1.00000000000000
sage: coefs = list(s1)
sage: print coefs
[1.00000000000000, -3.00000000000000, 2.00000000000000]
Ejercicio : Reconstruye el polinomio a partir de los coeficientes.
Ejemplo: [1,-3,3] ->