Álgebra lineal¶

Espacios vectoriales¶

En Sage podemos trabajar con distintos cuerpos para los coeficientes de los espacios vectoriales. Las elecciones más usuales son:

QQ (o RationalField() ) el cuerpo de los números racionales.

QQbar (o AlgebraicField () ), representa la clausura algebraica $\bar{\mathbb{Q}}$ del cuerpo de los números racionales.

RDF (o RealDoubleField() ), números reales de 64 bits.

CDF (o ComplexDoubleField() ), números complejos de 64 bits.

SR , o expresiones simbólicas. Cualquier expresión algebraica que contenga símbolos como pi, I, sqrt(2) pertenece a este anillo.

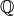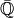Los cuerpos $\mathbb{Q}$ y $\bar{\mathbb{Q}}$ son computables, y sus implementaciones en Sage son exactas (en la documentación de Sage: “exact field”), es decir, los cálculos no acumulan errores de redondeo. Sin embargo, los tres últimos cuerpos no tienen aritmética exacta, debido a los errores de redondeo. Esto significa que en estos cuerpos no se pueden hacer cálculos como la multiplicidad de las raíces de un polinomio o la forma de Jordan de una matriz, que sean inestables ante la aparición de errores numéricos.

sage: V1 = VectorSpace(QQ,3)
sage: V2 = VectorSpace(RDF,3)    #Numeros reales de precision doble
sage: V3 = VectorSpace(CDF,4)    #Numeros complejos de precision doble
sage: print V1
sage: print V2
sage: print V3
Vector space of dimension 3 over Rational Field
Vector space of dimension 3 over Real Double Field
Vector space of dimension 4 over Complex Double Field

Vectores¶

Los vectores pertenecen a un espacio vectorial concreto, aunque SAGE hará las conversiones necesarias entre tipos de datos si queremos hacer operaciones entre espacios vectoriales compatibles.

sage: #O tambien
sage: v1 = V1([1,1,1])
sage: v2 = V2([1,1,0])
sage: v3 = 2*v1+v2
sage: print v1 ,v1.parent()
sage: print v2 ,v2.parent()
sage: print v3 ,v3.parent()
(1, 1, 1) Vector space of dimension 3 over Rational Field
(1.0, 1.0, 0.0) Vector space of dimension 3 over Real Double Field
(3.0, 3.0, 2.0) Vector space of dimension 3 over Real Double Field

sage: #pero...
sage: v1 = V1([1,1])
Traceback (most recent call last):
...
TypeError: entries must be a list of length 3

sage: #ni tampoco...
sage: v1 = V2([1,1,1])
sage: v2 = V3([1,1,0,0])
sage: v3 = v1+v2
Traceback (most recent call last):
...
TypeError: unsupported operand parent(s) for '+': 'Vector space of dimension 3 over Real Double Field' and 'Vector space of dimension 4 over Complex Double Field'

También podemos usar vector sin indicar el espacio vectorial, y entonces Sage escogerá como espacio ambiente el anillo de coeficientes más pequeño que contenga a las entradas. Si los coeficientes son enteros, como 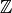$\mathbb{Z}$ no es un cuerpo, en vez de “espacio vectorial”, Sage habla de “modulo”, pero no es necesario preocuparnos por esa distinción.

sage: v1 = vector([1,1,1])
sage: v2 = vector([1/2,1,1])
sage: v3 = vector([1.0,1,0])
sage: print v1 ,v1.parent()
sage: print v2 ,v2.parent()
sage: print v3 ,v3.parent()
(1, 1, 1) Ambient free module of rank 3 over the principal ideal domain Integer Ring
(1/2, 1, 1) Vector space of dimension 3 over Rational Field
(1.00000000000000, 1.00000000000000, 0.000000000000000) Vector space of dimension 3 over Real Field with 53 bits of precision

Subespacios vectoriales¶

Podemos definir fácilmente el subespacio engrendrado por un conjunto de vectores, y después hacer operaciones como intersección o suma de subespacios, o comprobaciones como igualdad o inclusión de subespacios.

sage: v1 = vector([1,1,1])
sage: v2 = vector([1,1,0])
sage: v3 = vector([1,0,1])
sage: #Hay que fijarse en el cuerpo de coeficientes
sage: L1 = V1.subspace([v1,v2])
sage: L1_bis = V2.subspace([v1,v2])
sage: print L1
sage: print L1_bis
Vector space of degree 3 and dimension 2 over Rational Field
Basis matrix:
[1 1 0]
[0 0 1]
Vector space of degree 3 and dimension 2 over Real Double Field
Basis matrix:
[1.0 1.0 0.0]
[0.0 0.0 1.0]

El grado (degree) al que se refiere arriba, es la dimensión del espacio ambiente. Podemos recuperar este espacio directamente con el método ambient_vector_space .

sage: #Dimension
sage: print dim(L1)
2

sage: #Grado
sage: print L1.degree()
3

sage: L1.ambient_vector_space()
Vector space of dimension 3 over Rational Field

Muchos operadores actúan sobre subespacios vectoriales, con los significados habituales. Cuando el símbolo usual para la operación no está en el teclado (como el operador de intersección 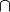$\cap$ ), lo normal es usar un método (como el método intersection ).

sage: #Pertenencia al subespacio
sage: print v3 in L1
sage: v4 = vector([4,4,3])
sage: print v4 in L1
False
True

sage: #Comprobacion de igualdad
sage: print L1 == V1
sage: print L1 == V1.subspace([v1,v1+v2])
False
True

sage: #Comprobacion de inclusion
sage: print L1 <= V1
sage: print L1 >= V1
sage: print L1 >= V1.subspace([v1])
True
False
True

Ejercicio resuelto¶

Definimos dos subespacios de 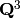$\Bold{Q}^{3}$ :

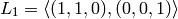
$L_1 =\left\langle(1, 1, 0), (0, 0, 1)\right\rangle$

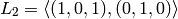
$L_2 =\left\langle(1, 0, 1), (0, 1, 0)\right\rangle$

Encuentra bases de los subespacios $L_1\cap L_2$ y $L_1+L_2$

sage: v1 = vector([1,1,0])
sage: v2 = vector([0,0,1])
sage: v3 = vector([1,0,1])
sage: v4 = vector([0,1,0])
sage: L1 = V1.subspace([v1,v2])
sage: L2 = V1.subspace([v3,v4])
sage: #Interseccion de subespacios
sage: L3 = L1.intersection(L2)
sage: print 'Intersección'
sage: print L3
sage: print
sage: #Suma de subespacios
sage: L4 = L1 + L2
sage: print 'Suma'
sage: print L4
sage: print L4 == V1
Intersección
Vector space of degree 3 and dimension 1 over Rational Field
Basis matrix:
[1 1 1]

Suma
Vector space of degree 3 and dimension 3 over Rational Field
Basis matrix:
[1 0 0]
[0 1 0]
[0 0 1]
True

Bases de los espacios vectoriales¶

Como hemos visto, al definir subespacios mediante generadores, se construye una base escalonada del subespacio a partir de los generadores. Para imponer la base del espacio o subespacio, usamos el comando subspace_with_basis .

sage: v1 = vector([1,1,0])
sage: v2 = vector([1,0,1])
sage: L1 = V1.subspace([v1,v2])
sage: print L1
sage: print L1.basis()
sage: print L1.basis_matrix()
Vector space of degree 3 and dimension 2 over Rational Field
Basis matrix:
[ 1  0  1]
[ 0  1 -1]
[
(1, 0, 1),
(0, 1, -1)
]
[ 1  0  1]
[ 0  1 -1]

sage: L1 = V1.subspace([v1,v2])
sage: L2 = V1.subspace([v1,v1+v2])
sage: print L1.basis()
sage: print L2.basis()
[
(1, 0, 1),
(0, 1, -1)
]
[
(1, 0, 1),
(0, 1, -1)
]

sage: L3 = V1.subspace_with_basis([v1,v2])
sage: print L1
sage: print L3
sage: #A pesar de tener distintas bases, ambos subespacios se declaran iguales
sage: print L1 == L3
sage: print L3.basis_matrix()
Vector space of degree 3 and dimension 2 over Rational Field
Basis matrix:
[ 1  0  1]
[ 0  1 -1]
Vector space of degree 3 and dimension 2 over Rational Field
User basis matrix:
[1 1 0]
[1 0 1]
True
[1 1 0]
[1 0 1]

El método coordinates nos da las coordenadas de un vector en la base del espacio.

sage: print L1.coordinates(2*v1+3*v2)
sage: print L2.coordinates(2*v1+3*v2)
sage: print L3.coordinates(2*v1+3*v2)
[5, 2]
[5, 2]
[2, 3]

Matrices¶

Para crear una matriz manualmente en SAGE, llamamos a matrix con el anillo de coeficientes como primer argumento. Después introducimos los datos usando una de las dos formas siguientes:

Como una lista de listas, cada una de las cuales contiene una fila de la matriz:

   #Matriz 2x4 con coeficientes en Q
   M = matrix(QQ,[[0,1,0,0],[1,0,0,0]])





- Pasando el número de filas, el de columnas, y una sóla lista con todos los elementos:

M = matrix(QQ, K1, K2, lista)

donde K1 es el número de filas y K2 el número de columnas y, en vez de pasar una lista con las filas, pasamos una sóla lista con K1xK2 elementos:

matrix(QQ, 2, 4, [1,2,3,4,5,6,7,8])

sage: M1 = matrix(QQ,[[1,2,3,4],[4,2,3,1]])
sage: M2 = matrix(QQ,3,3,[3,2,1,  1,2,3,  2,2,2])
sage: show(M1)
sage: show(M2)

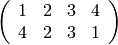
$\left(\begin{array}{rrrr} 1 & 2 & 3 & 4 \\ 4 & 2 & 3 & 1 \end{array}\right)$

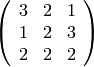
$\left(\begin{array}{rrr} 3 & 2 & 1 \\ 1 & 2 & 3 \\ 2 & 2 & 2 \end{array}\right)$

Métodos de las matrices¶

Aparte de los cálculos habituales con matrices, como determinante o rango, hay otros métodos interesantes que conectan con lo visto antes. Mencionamos tres, pero recuerda que puedes ver una lista completa escribiendo el nombre de tu matriz seguido de un punto y pulsando el tabulador:

M.kernel() : Núcleo de una matriz, visto como un subespacio vectorial (pon atención a la diferencia entre el kernel por la izquierda M.left_kernel() o por la derecha M.right_kernel() ; el método kernel a secas se corresponde con left_kernel )

M.image() : Imagen de una matriz, como subespacio vectorial

M.echelon_form() : forma escalonada

sage: M1 = matrix(QQ,[[1,2,3,4],[4,2,3,1]])
sage: show(M1)
sage: print M1.kernel()   #lo mismo que M1.left_kernel()
sage: print
sage: print M1.image()
sage: show( M1.echelon_form())
Vector space of degree 2 and dimension 0 over Rational Field
Basis matrix:
[]

Vector space of degree 4 and dimension 2 over Rational Field
Basis matrix:
[  1   0   0  -1]
[  0   1 3/2 5/2]

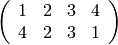
$\left(\begin{array}{rrrr} 1 & 2 & 3 & 4 \\ 4 & 2 & 3 & 1 \end{array}\right)$

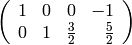
$\left(\begin{array}{rrrr} 1 & 0 & 0 & -1 \\ 0 & 1 & \frac{3}{2} & \frac{5}{2} \end{array}\right)$

sage: M2 = matrix(QQ,3,3,[3,2,1,  5,2,1,  4,2,1])
sage: show(M2)
sage: print M2.kernel()
sage: print
sage: print M2.image()
Vector space of degree 3 and dimension 1 over Rational Field
Basis matrix:
[ 1  1 -2]

Vector space of degree 3 and dimension 2 over Rational Field
Basis matrix:
[  1   0   0]
[  0   1 1/2]

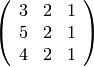
$\left(\begin{array}{rrr} 3 & 2 & 1 \\ 5 & 2 & 1 \\ 4 & 2 & 1 \end{array}\right)$

sage: #Una matriz invertible 4x4
sage: M3 = matrix(CDF, [[ 2,  0, -2,  2], [ 1,  3,  2, -3], [ 5,  1,  8, -3], [ 5,  1,  4,  1]])
sage: show(M3)
sage: print M3.kernel()
sage: print
sage: print M3.image()
Vector space of degree 4 and dimension 0 over Complex Double Field
Basis matrix:
[]

Vector space of degree 4 and dimension 4 over Complex Double Field
Basis matrix:
[1.0   0   0   0]
[  0 1.0   0   0]
[  0   0 1.0   0]
[  0   0   0 1.0]

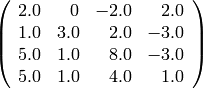
$\left(\begin{array}{rrrr} 2.0 & 0 & -2.0 & 2.0 \\ 1.0 & 3.0 & 2.0 & -3.0 \\ 5.0 & 1.0 & 8.0 & -3.0 \\ 5.0 & 1.0 & 4.0 & 1.0 \end{array}\right)$

Suma y productos de matrices¶

La suma de matrices y productos por vectores se comporta de la manera previsible, lanzando errores si las dimensiones no casan, y cambiando los tipos de datos según sea necesario para hacer operaciones cuyos operandos tienen coeficientes en cuerpos distintos, pero compatibles.

sage: M4 = identity_matrix(QQ, 4)
sage: show(M4)
sage: show(3*M4 + M3)

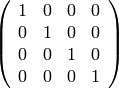
$\left(\begin{array}{rrrr} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right)$

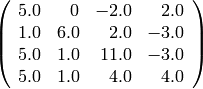
$\left(\begin{array}{rrrr} 5.0 & 0 & -2.0 & 2.0 \\ 1.0 & 6.0 & 2.0 & -3.0 \\ 5.0 & 1.0 & 11.0 & -3.0 \\ 5.0 & 1.0 & 4.0 & 4.0 \end{array}\right)$

sage: v = vector(CDF,[-1, 0.5, -0.5, 2 ])
sage: print M3*v
sage: print M3*v + 2*v
(3.0, -6.5, -14.5, -4.5)
(1.0, -5.5, -15.5, -0.5)

sage: #Ejemplo: dos matrices cuadradas que no conmutan
sage: M1 = matrix(QQ,2,2,[1,1,0,1])
sage: M2 = matrix(QQ,2,2,[2,0,0,1])
sage: show(M1*M2)
sage: show(M2*M1)

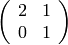
$\left(\begin{array}{rr} 2 & 1 \\ 0 & 1 \end{array}\right)$

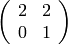
$\left(\begin{array}{rr} 2 & 2 \\ 0 & 1 \end{array}\right)$

Obtener el subespacio dado por ecuaciones¶

Si tenemos un espacio dado por ecuaciones, basta poner los coeficientes de las ecuaciones en una matriz, y podemos obtener el subespacio que define como el conjunto de vectores en los que todas las ecuaciones se anulan (es decir el núcleo). Por ejemplo, escribimos las ecuaciones

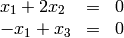
$\begin{array}{lll} x_1 + 2 x_2 & = & 0 \\ - x_1 + x_3 & = & 0 \end{array}$

en forma matricial:

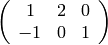
$\left(\begin{array}{ccc} 1 & 2 & 0 \\ - 1 & 0 & 1 \end{array}\right)$

Al haber elegido esta forma de escribir la matriz, el espacio que nos interesa es el kernel por la derecha ( right_kernel )

sage: M = matrix(QQ,2,3,[1,2,0, -1,0,1])
sage: M.right_kernel()
Vector space of degree 3 and dimension 1 over Rational Field
Basis matrix:
[   1 -1/2    1]

Obtener las ecuaciones de un subespacio¶

Si tenemos un subespacio, podemos obtener unas ecuaciones de esta forma:

el método basis_matrix() devuelve una matriz que contiene los vectores de una base

las ecuaciones del subespacio son los covectores que se anulan en esos vectores (es decir, el núcleo de la matriz anterior), que obtenemos con right_kernel()

Una base del núcleo nos da un conjunto minimal de ecuaciones que define el subespacio.

Ejercicio resuelto¶

Encuentra las ecuaciones del subespacio de 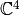$\mathbb{C}^{4}$ engendrado por $[1,1,1,1]$ y $[1,1,0,0]$

sage: v1 = vector([1,1,1,1])
sage: v2 = vector([1,1,0,0])
sage: L1 = V3.subspace([v1,v2])

sage: #Ecuaciones del subespacio
sage: M = L1.basis_matrix()
sage: K = M.right_kernel()
sage: print K.basis()
[
(1.0, -1.0, 0, 0),
(0, 0, 1.0, -1.0)
]

Ejercicio resuelto¶

Encuentra una base del subespacio de 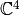$\mathbb{C}^{4}$ dado por 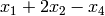$x_1+2x_2-x_4$ y una base de su intersección con el subespacio engendrado por $[1,1,1,1]$ y $[1,1,0,0]$ .

sage: #Subespacio dado por x1 + 2*x2 -x4 en V(CDF,4)
sage: M = matrix(CDF,4,1,[1,2,0,-1])
sage: show(M)
sage: L2 = M.left_kernel()
sage: print L2
Vector space of degree 4 and dimension 3 over Complex Double Field
Basis matrix:
[1.0   0   0 1.0]
[  0 1.0   0 2.0]
[  0   0 1.0   0]

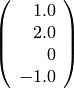
$\left(\begin{array}{r} 1.0 \\ 2.0 \\ 0 \\ -1.0 \end{array}\right)$

sage: L1.intersection(L2)
Vector space of degree 4 and dimension 1 over Complex Double Field
Basis matrix:
[1.0 1.0 3.0 3.0]

Autovalores, autoespacios, forma de Jordan¶

Como indicamos arriba, la forma de Jordan es inestable antes pequeños errores. Esto hace imposible calcular la forma de Jordan usando aritmética aproximada con errores de redondeo. La elección del cuerpo de coeficientes se vuelve por tanto muy importante.

sage: M = matrix(QQ,3,3,[0,1,0,1,0,0,0,0,1])
sage: print M
sage: print M.eigenvalues()
sage: show( M.eigenvectors_left())
sage: print M.jordan_form()
[0 1 0]
[1 0 0]
[0 0 1]
[-1, 1, 1]
[-1| 0| 0]
[--+--+--]
[ 0| 1| 0]
[--+--+--]
[ 0| 0| 1]

$\left[\left(-1, \left[\left(1,-1,0\right)\right], 1\right), \left(1, \left[\left(1,1,0\right), \left(0,0,1\right)\right], 2\right)\right]$

sage: M = matrix(QQ,3,3,[ 8,  6,  3, -1,  8, -3, 4, 10, 19])
sage: show(M)
sage: print M.eigenvalues()
sage: show( M.eigenvectors_left())
sage: print M.jordan_form()
[7, 14, 14]
[ 7| 0  0]
[--+-----]
[ 0|14  1]
[ 0| 0 14]

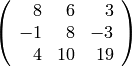
$\left(\begin{array}{rrr} 8 & 6 & 3 \\ -1 & 8 & -3 \\ 4 & 10 & 19 \end{array}\right)$

$\left[\left(7, \left[\left(1,-1,-\frac{1}{2}\right)\right], 1\right), \left(14, \left[\left(1,6,3\right)\right], 2\right)\right]$

También podemos obtener la matriz de paso:

sage: M = matrix(QQ,3,3,[ 8,  6,  3, -1,  8, -3, 4, 10, 19])
sage: M.jordan_form(transformation=True)
(
[ 7| 0  0]
[--+-----]  [   1    0    1]
[ 0|14  1]  [   0   -7    0]
[ 0| 0 14], [-1/3   14    2]
)

La siguiente matriz tiene autovalores en 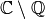$\mathbb{C}\setminus\mathbb{Q}$

sage: M = matrix(QQ,3,3,[0,1,0,-1,0,0,0,0,1])
sage: print M
sage: print M.eigenvalues()
sage: show( M.eigenvectors_left())
[ 0  1  0]
[-1  0  0]
[ 0  0  1]
[1, -1*I, 1*I]

$\left[\left(1, \left[\left(0,0,1\right)\right], 1\right), \left(\hbox{-1*I}, \left[\left(1,\hbox{1*I},0\right)\right], 1\right), \left(\hbox{1*I}, \left[\left(1,\hbox{-1*I},0\right)\right], 1\right)\right]$

sage: print M.jordan_form()
Traceback (most recent call last):
...
RuntimeError: Some eigenvalue does not exist in Rational Field.

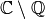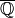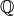Como vemos, si hay autovalores en $\mathbb{C}\setminus\mathbb{Q}$ , SAGE no calcula la forma de Jordan. Una solución es ampliar los coeficientes a $\overline{\mathbb{Q}}$ , el cuerpo de los números algebraicos, que contiene todas las raíces de ecuaciones con coeficientes en $\mathbb{Q}$ .

sage: #El cuerpo QQbar contiene las raices de todos los
sage: #polinomios con coeficientes en QQ
sage: M2 = M.base_extend(QQbar)
sage: print M2.jordan_form()
[   1|   0|   0]
[----+----+----]
[   0|-1*I|   0]
[----+----+----]
[   0|   0| 1*I]

La forma de Jordan sólo está definida en anillos de coeficientes exactos, como QQ, o QQbar, pero no tiene sentido en anillos con precisión limitada, porque la forma de Jordan es numéricamente inestable. Intentar calcular una forma de Jordan en un cuerpo con errores numéricos simplemente genera un error.

sage: M = matrix(CDF,3,3,[ 8,  6,  3, -1,  8, -3, 4, 10, 19])
sage: print M.jordan_form()
Traceback (most recent call last):
...
ValueError: Jordan normal form not implemented over inexact rings.

Los autoespacios también son problemáticos, y es mejor evitarlos, si usamos aritmética aproximada.

sage: M = matrix(QQ,2,2,[ 1, 1, 0, 1])
sage: print M.eigenspaces_right()
[
(1, Vector space of degree 2 and dimension 1 over Rational Field
User basis matrix:
[0 1])
]

sage: M = matrix(CDF,2,2,[ 1, 1, 0, 1])
sage: print M.eigenspaces_right()
__main__:4: DeprecationWarning: Eigenspaces of RDF/CDF matrices are
deprecated as of Sage version 5.0, please use "eigenmatrix_left" instead
See http://trac.sagemath.org/11603 for details.
[(1.0, Vector space of degree 2 and dimension 1 over Complex Double
Field
User basis matrix:
[-2.22044604925e-16                1.0]), (1.0, Vector space of degree 2
and dimension 1 over Complex Double Field
User basis matrix:
[0.0 1.0])]

Sin embargo, aunque trabajemos con números de coma flotante, todavía tiene sentido hablar de autovalores:

sage: M = matrix(CDF,3,3,[ 8,  6,  3, -1,  8, -3, 4, 10, 19])
sage: print M.eigenvalues()
[7.0 - 9.39502740013e-17*I, 14.0000000001 + 1.5006305546e-07*I, 13.9999999999 - 1.5006304995e-07*I]

También podemos seguir el consejo que nos dieron al llamar al método eigenspaces_right() de una matriz con coeficientes en CDF, y usar el método eigenmatrix_right()...

Álgebra lineal¶

Espacios vectoriales¶

Vectores¶

Subespacios vectoriales¶

Ejercicio resuelto¶

Bases de los espacios vectoriales¶

Matrices¶

Métodos de las matrices¶

Suma y productos de matrices¶

Obtener el subespacio dado por ecuaciones¶

Obtener las ecuaciones de un subespacio¶

Ejercicio resuelto¶

Ejercicio resuelto¶

Autovalores, autoespacios, forma de Jordan¶

Contenidos

Tema anterior

Próximo tema

Esta página

Navegación

Álgebra lineal¶

Espacios vectoriales¶

Vectores¶

Subespacios vectoriales¶

Ejercicio resuelto¶

Bases de los espacios vectoriales¶

Matrices¶

Métodos de las matrices¶

Suma y productos de matrices¶

Obtener el subespacio dado por ecuaciones¶

Obtener las ecuaciones de un subespacio¶

Ejercicio resuelto¶

Ejercicio resuelto¶

Autovalores, autoespacios, forma de Jordan¶

Contenidos

Tema anterior

Próximo tema

Esta página

Búsqueda rápida

Navegación