Ejercicios¶

1.¶

Busca las ecuaciones (paramétricas, implícitas o las que más te convengan) de las siguientes curvas y dibújalas:

Lemniscata de Bernouilli

Tractriz

Cicloide

2.¶

Compara las distintas formas de representar la misma curva usando parametric_plot , polar_plot e implicit_plot para comprobar que se obtiene el mismo resultado:

Las ecuaciones implícitas de la recta $Ax+By=1$ y la forma polar vista en clase.

Las ecuaciones implícitas de la circunferencia $(x-x_0)^2+(y-y_0)^2=r^2$ que pasa por el origan y la forma polar vista en clase.

Busca las ecuaciones implícitas de la curva de Agnesi y comprueba que corresponde a la misma curva que la parametrización vista en clase.

Idem para el folium de Descartes.

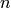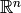3. Ecuación de un hiperplano en el espacio $n$ -dimensional $\mathbb{R}^n$ ¶

Si denotamos por 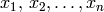$x_1,\,x_2,\dots,x_n$ las coordenadas cartesianas en 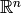$\mathbb R^n$ , una ecuación implícita o cartesiana del hiperplano determinado por 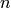$n$ puntos, 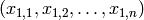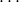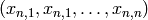$(x_{1,1}, x_{1,2},\dots,x_{1,n})$ , $\dots$ , $(x_{n,1}, x_{n,1},\dots,x_{n,n})$ , en posición general , se obtiene al desarrollar:

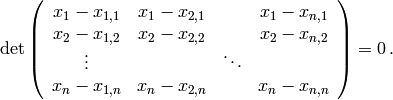
$\mathrm{det}\left(\begin{array}{cccc}x_1-x_{1,1} & x_1-x_{2,1} && x_1-x_{n,1}\\ x_2-x_{1,2} & x_2-x_{2,2}& & x_2-x_{n,2} \\ \vdots & &\ddots \\ x_n-x_{1,n} & x_n-x_{2,n} & &x_n-x_{n,n}\end{array}\right)=0\,.$

Al simplificar el desarrollo, el vector, 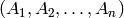$(A_1,A_2,\dots,A_n)$ , formado por los coeficientes en la ecuación 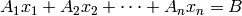$A_1x_1+A_2x_2+\dots+A_nx_n=B$ es perpendicular al hiperplano (vector normal del hiperplano).

Obtén la ecuación implícita del plano que pasa por 3 puntos de $\mathbb{R}$ .

4.¶

Encuentra 5 puntos tal que la cónica que pasa por ellos sea una hipérbola, una parábola, y el producto de 2 rectas (no importa que no estén en posición general).

5. Explorando el comando `animate` .¶

El comando animate permite convertir una lista de gráficas en una animación cuyos fotogramas son las gráficas de la lista.

Investiga la ayuda de animate, y encuentra el código que muestra la gráfica del seno desplazándose a lo largo del eje x.

Crea una animación de un punto moviéndose desde un punto A a otro punto B.

Crea una animación de un punto moviéndose a lo largo de una circunferencia de centro (0,0) y radio 1.

6.¶

Combina lo aprendido sobre el comando animate con lo visto en clase de teoría para crear una animación del haz de cónicas que pasa por 4 puntos.

7.¶

Dada una curva 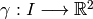$\gamma: I\longrightarrow \mathbb R^2$ dada por 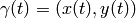$\gamma(t)= (x(t),y(t))$ , el vector tangente a la curva en 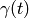$\gamma(t)$ es el vector con origen en 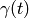$\gamma(t)$ y dirección 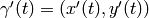$\gamma'(t)= (x'(t),y'(t))$ . Investiga el método arrow y dibuja el vector tangente en varias de las curvas definidas en coordenadas paramétricas en la clase de teoría.

8.¶

Combina lo aprendido sobre el comando animate con el ejercicio anterior para hacer animaciones donde la curva está fija y el vector tangente se mueve a lo largo de la curva.

Ejercicios¶

1.¶

2.¶

3. Ecuación de un hiperplano en el espacio $n$ -dimensional $\mathbb{R}^n$ ¶

4.¶

5. Explorando el comando `animate` .¶

6.¶

7.¶

8.¶

Contenidos

Tema anterior

Próximo tema

Esta página

Navegación

Ejercicios¶

1.¶

2.¶

3. Ecuación de un hiperplano en el espacio -dimensional ¶

4.¶

5. Explorando el comando animate .¶

6.¶

7.¶

8.¶

Contenidos

Tema anterior

Próximo tema

Esta página

Búsqueda rápida

Navegación

3. Ecuación de un hiperplano en el espacio $n$ -dimensional $\mathbb{R}^n$ ¶

5. Explorando el comando `animate` .¶