En esta sesión vamos a utilizar varios métodos de representación de curvas en el plano:
- en paramétricas;
- en coordenadas polares;
- por una ecuación implícita.
Pensaremos en una curva plana como la imagen por una función continua 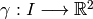 , con I un intervalo de números reales. Si tomamos
, con I un intervalo de números reales. Si tomamos 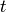 como variable independiente (
como variable independiente (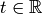 ), describiremos la imagen como el conjunto de puntos
), describiremos la imagen como el conjunto de puntos
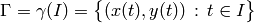
o simplemente
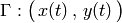
Cuando el dominio de valores para el parámetro 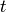 es un intervalo, digamos
es un intervalo, digamos ![[a,b]](_images/math/8ecbd1ba3da8f2adef66a63f2ab32c47e63fa734.png) , la curva tiene como extremos los puntos:
, la curva tiene como extremos los puntos: 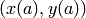 y
y 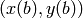 .
.
- La curva
, para
, es el segmento de recta que une los puntos
y
. En general, si
y
son dos puntos, un segmento rectilíneo que une
con
es:
, considerando
.
Antes de continuar, vamos a utilizar Sage para ‘ dibujar ‘ este ejemplo. Necesitamos que nuestro código sepa interpretar la expresión 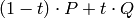 como lo haríamos nosotros, a saber: si
como lo haríamos nosotros, a saber: si 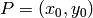 y
y 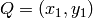 , el resultado queda:
, el resultado queda:
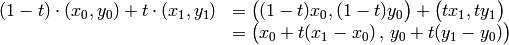
Esta manipulación (afín), no es más que tratar a los puntos 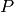 y
y 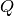 como vectores (los vectores
como vectores (los vectores 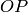 y
y 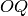 , cuando se ha fijado un punto como origen del plano afín). En el siguiente código se consigue este propósito. Utilizamos la función parametric_plot de Sage (leer la ayuda antes de seguir). Obsérvese en qué manera se explicita el intervalo para la variable
, cuando se ha fijado un punto como origen del plano afín). En el siguiente código se consigue este propósito. Utilizamos la función parametric_plot de Sage (leer la ayuda antes de seguir). Obsérvese en qué manera se explicita el intervalo para la variable 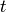 .
.
sage: parametric_plot?
<html>...</html>
sage: # Segmento rectilíneo entre dos puntos P y Q
sage: var('t')
sage: P=vector((1,-1))
sage: Q=vector((2,2))
sage: #Observación
sage: show((1-t)*P+t*Q)
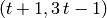
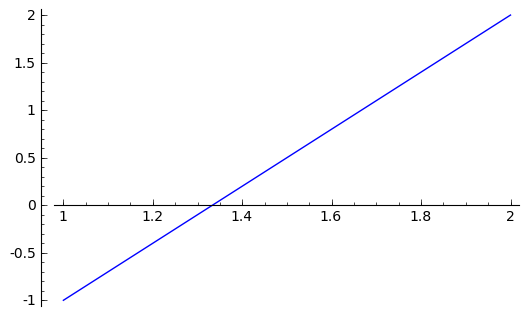
sage: parametric_plot((1-t)*P+t*Q, (t, 0, 1))
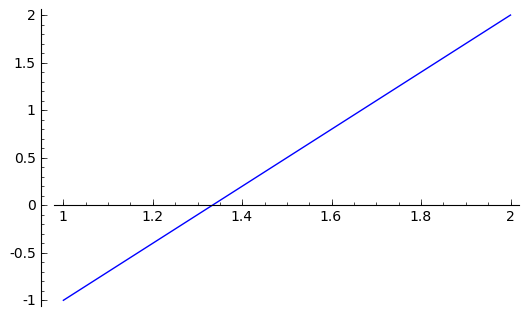
sage: parametric_plot( (t + 1, 3*t - 1) , (t, 0, 1))
- Si tenemos una función (continua) real de variable real,
, la gráfica es una curva en el plano,
, que podemos presentar paramétricamente (tomando
). Estos son casos particulares de curvas, en las que no hay más de un punto en cada vertical (¿por qué?).
- Una parábola:
- Una exponencial:
- Curvas trigonométricas:
,
,
- Funciones racionales:
,
. En los puntos en que una función tal no es continua, la gráfica no es fiel (comprobarlo).
- Polinomios, ...
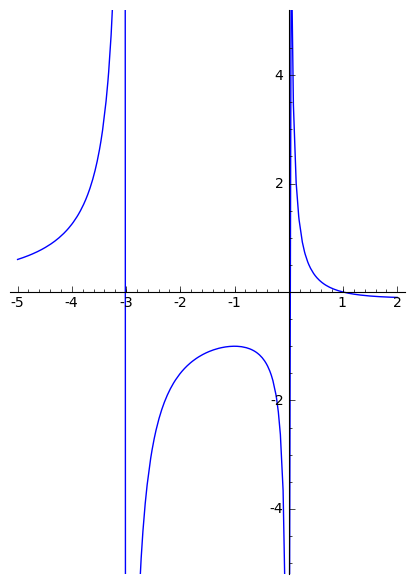
sage: p = parametric_plot((t,(1-t)/(t^2+3*t)), (t,-5,2))
sage: p.show(ymin=-5, ymax=5)
La mayoría del lenguaje de curvas parametrizadas viene del estudio del movimiento de una partícula. En esos casos, el parámetro de la curva suele ser el tiempo (¡qué buena elección de letra 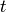 !), y cada punto de la curva marca la posición de la partícula en cada momento. Así el segmento rectilíneo entre dos puntos
!), y cada punto de la curva marca la posición de la partícula en cada momento. Así el segmento rectilíneo entre dos puntos 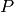 y
y 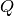 descrito por
descrito por ![\Gamma: (1-t)\cdot P+t\cdot Q,\,t\in[0,1]](_images/math/3e80d247140d1e5d624932fa5ce5275554d45ad1.png) sería la trayectoria descrita por una partícula que viaja en línea recta, partiendo de
sería la trayectoria descrita por una partícula que viaja en línea recta, partiendo de 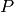 y llegando a
y llegando a 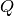 en una unidad de tiempo (
en una unidad de tiempo (![t\in[0,1]](_images/math/e70754c1efb07bd54438989e7e001bafb98b429a.png) ).
).
Este enfoque nos surte de una cantidad tremenda de ejemplos, históricamente estudiados por grandes físicos y matemáticos, de los que a continuación exponemos una brevísima lista (para ver más visitar, por ejemplo: mathcurve.com , epsilones.com ):
- Circunferencia (centrada en el origen y de radio
):
- Bruja de Agnesi:
(
es el radio de la circunferencia base —ver construcción más abajo)
- Astroide:
,
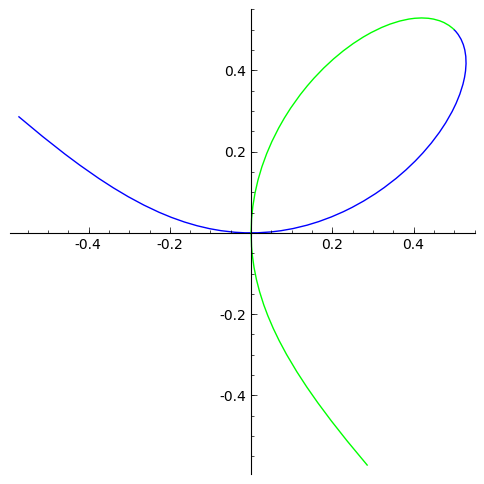
- El folium de Descartes:
,
. Nota: el cambio
por
, cambia
e
.
- ???:
sage: # Dibujamos el folium de Descartes pegando dos ramas simétricas respecto al eje (y=x).
sage: rama1=parametric_plot((t/(1+t^3),t^2/(1+t^3)), (t,-.5,1))
sage: rama2=parametric_plot((t^2/(1+t^3),t/(1+t^3)), (t,-.5,1), color=(0,1,0))
sage: show(rama1+rama2, aspect_ratio=1)
sage: #Cúbica (o bruja) de Agnesi
sage: var('t theta x y')
sage: a = 1
sage: bruja = parametric_plot((2*a*t,2*a/(t^2+1)), (t, -2, 2))
sage: #circle dibuja una circunferencia de centro y radio dados
sage: circ_bruja = circle((0,a),a)
sage: ambas = bruja + circ_bruja
sage: show(ambas, aspect_ratio=1)
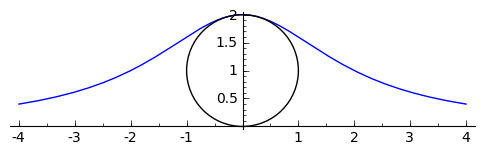
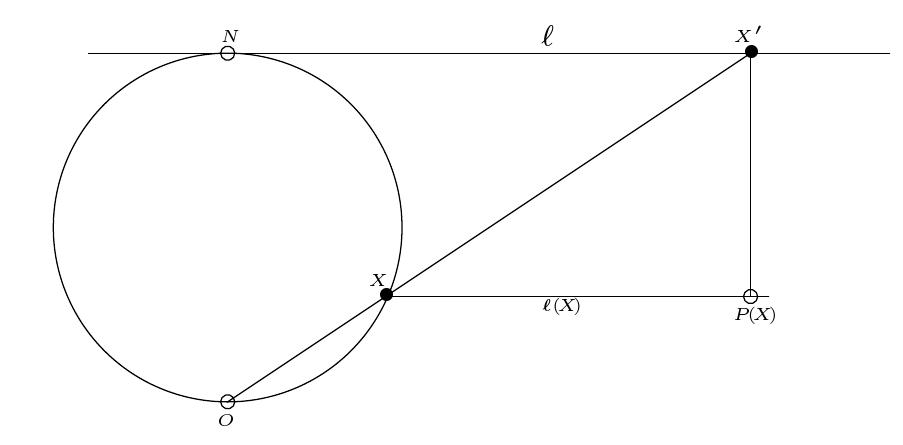
Se consideran dos puntos diametralmente opuestos en una circunferencia, 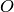 y
y 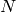 , y la tangente,
, y la tangente, 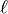 , a la circunferencia por uno de ellos, digamos que por
, a la circunferencia por uno de ellos, digamos que por 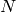 . Desde el otro, hacemos la siguiente construcción
. Desde el otro, hacemos la siguiente construcción
- para cada punto de la circunferencia,
, tomamos el punto de corte de la recta
con la recta
:
;
- completamos un triángulo rectángulo con
,
y un tercer punto,
, en la recta,
, paralela a
por el punto
: el ángulo recto sobre el vértice nuevo,
.
- La curva de Agnesi es la descrita por los puntos
.
sage: var('a t s x y')
(a, t, s, x, y)
sage: solve((2*a*t*s)^2+(2*a*s-a)^2-a^2,s)
[s == (1/(t^2 + 1)), s == 0]
Una manera alternativa de indicar la posición de cada punto es mediante sus coordenadas polares 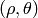 , siendo
, siendo 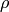 la distancia del punto al origen, y
la distancia del punto al origen, y 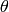 el ángulo que forma el vector que une el origen con el punto y el semieje horizontal positivo, es decir: si
el ángulo que forma el vector que une el origen con el punto y el semieje horizontal positivo, es decir: si 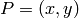

Obsérvese que la función 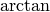 nos devuelve el valor correcto del ángulo salvo, quizás, un error de
nos devuelve el valor correcto del ángulo salvo, quizás, un error de 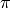 (pues
(pues 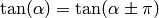 ). El cambio inverso, de polares a cartesianas, es más preciso:
). El cambio inverso, de polares a cartesianas, es más preciso:

Es claro que 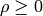 así como que basta tomar ángulos
así como que basta tomar ángulos 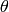 en el intervalo
en el intervalo 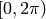 , por ejemplo.
, por ejemplo.
Para dar la ecuación en polares de una curva, se suele expresar el radio como una función del ángulo, pero se representa en el plano cartesiano. Así, si dibujamos la curva 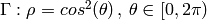 , estaremos dibujando los puntos del plano
, estaremos dibujando los puntos del plano 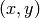 , con
, con 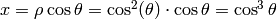 , e
, e 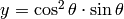 , variando
, variando 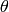 , en este caso, entre
, en este caso, entre 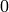 y
y 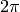 .
.
La función de Sage que utilizamos en este caso es polar_plot (revisar su ayuda en línea), que es equivalente a utilizar el valor polar=True en un plot() .
sage: polar_plot?
<html>...</html>
sage: var('theta')
sage: polar_plot(cos(theta)^2, (theta,0,2*pi))

- Recta de ecuación
(no pasa por el origen). Si
y
es el ángulo definido por
,
, entonces:
es su ecuación en polares.
- Recta que pasa por el origen: en este caso la descripción es más sencilla, pues todos los puntos de la recta (al unirse al origen) forman un ángulo constante con el eje de abcisas. Así, si dicho ángulo es
la ecuación es
. Ahora bien, no podemos indicarle a Sage cómo dibujarlas utilizando polar_plot() (ocurre como en la representación de rectas verticales,
, en coordenadas cartesianas).
Como vemos, las rectas no son muy amigables para representar en polares. Sigamos con ejemplos más enriquecedores.
- Circunferencia (con centro el origen):
,
. Y si el ángulo lo variamos menos, conseguimos cualquier arco de circunferencia.
- Circunferencia que pasa por el origen:
,
. Nota: el centro es el punto de coordenadas cartesianas
.
- Cónica con un foco en el origen: la ecuación de la cónica, dado un foco, necesita conocer la recta directriz y la excentricidad
. Si tal recta tiene ecuación cartesiana
, la cónica es el lugar de puntos
tales que
, siendo
la proyección ortogonal de
sobre la directriz. En tal caso, la ecuación polar de la cónica queda:
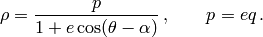
La recta 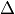 de ecuación
de ecuación 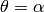 es eje de simetría. Cuando
es eje de simetría. Cuando 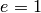 la cónica es una parábola,
la cónica es una parábola, 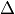 su eje de simetría y
su eje de simetría y 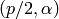 su vértice. Cuando
su vértice. Cuando 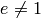 la cónica es una cónica con centro,
la cónica es una cónica con centro, 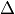 el eje focal y sus vértices se calculan sustituyendo
el eje focal y sus vértices se calculan sustituyendo 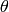 por
por 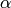 y
y 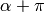 .
.
Por último una lista de curvas famosas con sus ecuaciones polares:
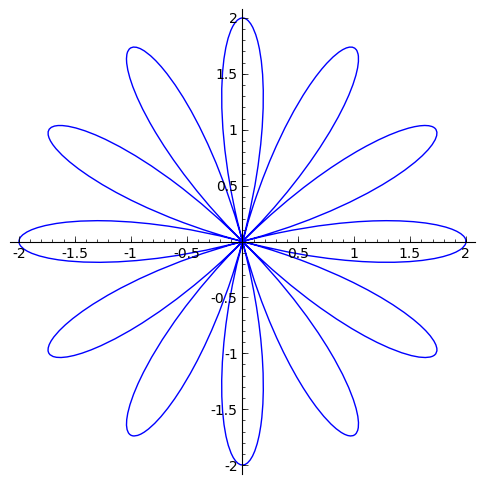
- Rosas:
,
. Ejercicio : averiguar el número de pétalos para cada valor natural de
. Nota:
puede ser cualquier real positivo.
- La cardiode:
,
.
- La cisoide:
,
.
- La estrofoide:
,
.
- La lemniscata de Bernoulli:
,
.
- Espirales:
- Espiral de Arquímedes:
,
.
- Espiral hiperbólica:
,
.
- Espiral logarítmica:
,
.
sage: rosas=polar_plot(2*cos(6*theta), (theta,0,2*pi))
sage: show(rosas, aspect_ratio=1)
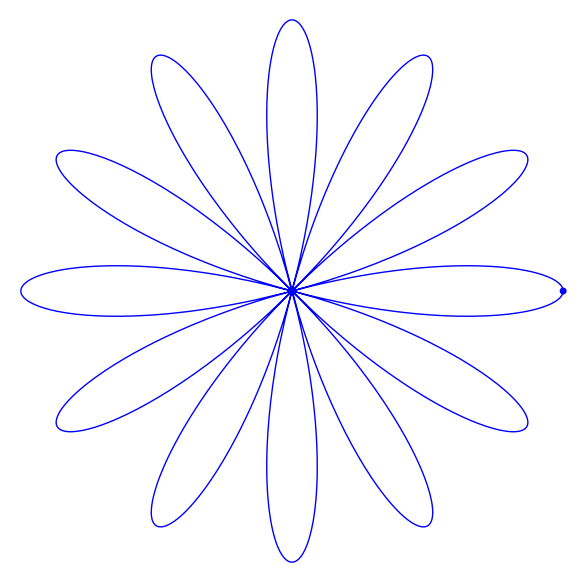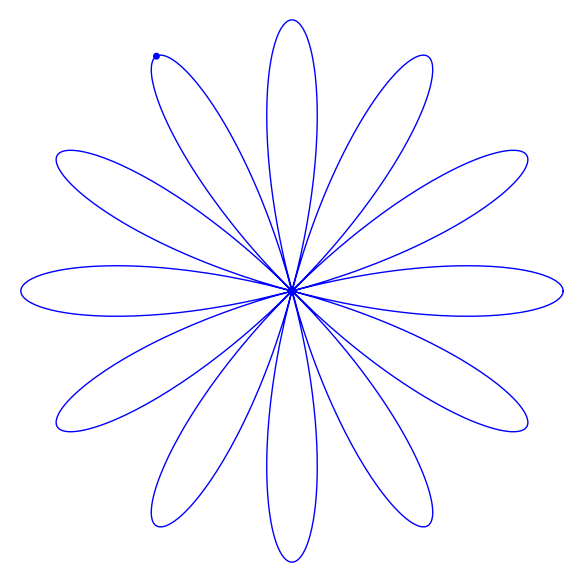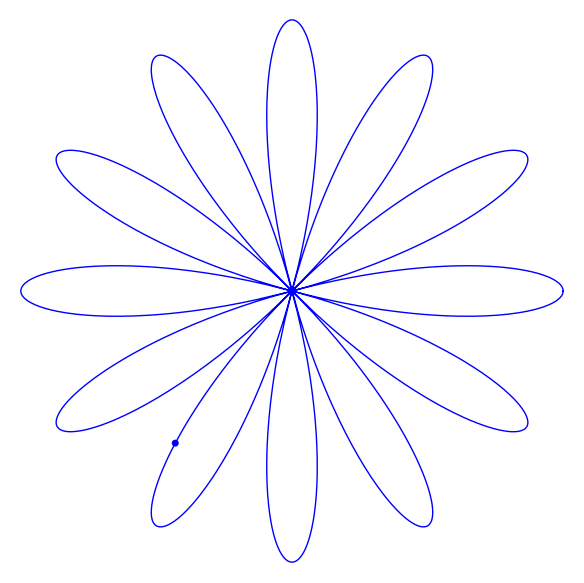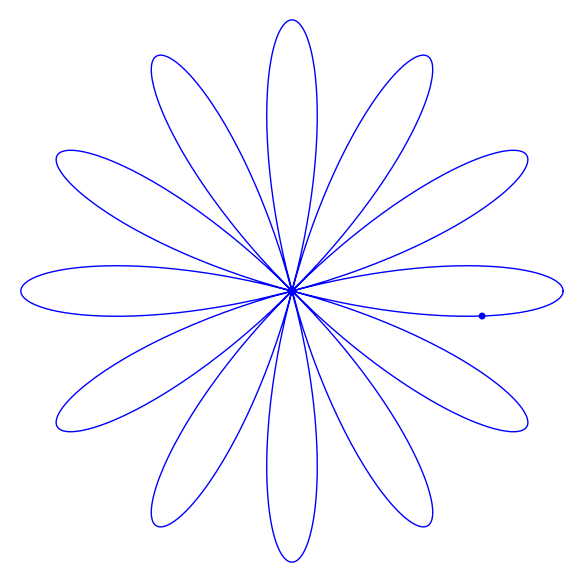
var('theta')
a,b=0,2*pi
n=48 ## puntos a mostrar
h=(b-a)/n ## equidistantes en el intervalo original
ro(theta)=2*cos(6*theta)
xx(theta)=ro(theta)*cos(theta) ## x-Cartesiana
yy(theta)=ro(theta)*sin(theta) ## y-Cartesiana
rosa=polar_plot(ro(theta), (theta,a,b), figsize=3, axes=false)
camino=[] ## inicio de la lista de fotogramas
for k in srange(a,b,h):
camino.append(rosa+point((xx(k),yy(k)), size=25))
a=animate(camino, figsize=(6,6))
a.show()
Aunque no han dejado de usarse, hasta aquí no hemos pedido a Sage que represente una curva cuyas ‘ecuaciones’ le vienen dadas en función de sus coordenadas cartesianas. Lo hasta ahora habitual es encontrarnos con que la coordenada 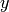 es una función de la coordenada
es una función de la coordenada 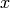 :
: 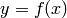 . Las herramientas del cálculo diferencial nos ayudan a esbozar este tipo de gráficas. En este apartado vamos a adoptar un punto de vista más general, dando una ecuación de la curva en la que ambas variables puedan aparecer en la expresión sin que sea necesario despejar una en función de la otra.
. Las herramientas del cálculo diferencial nos ayudan a esbozar este tipo de gráficas. En este apartado vamos a adoptar un punto de vista más general, dando una ecuación de la curva en la que ambas variables puedan aparecer en la expresión sin que sea necesario despejar una en función de la otra.
- La ecuación
, con
y
números reales, nos sirve para describir todos los puntos del plano cuyas coordenadas,
, la verifican. Es fácil comprobar que todos estos puntos quedan alineados, es decir describen una línea recta. De la ecuación dada decimos que es su ecuación cartesiana o implícita , y basta, para calcularla con dar dos puntos de la recta, o un punto y una dirección (vector director).
- Una ecuación implícita de la recta que pasa por los puntos de coordenadas
,
surge de desarrollar la siguiente igualdad:
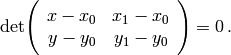
- Si conocemos que la recta pasa por el punto de coordenadas
y la dirección de la recta es la del vector
, una ecuación implícita la obtenemos al desarrollar:
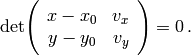
- Con ambos puntos de vista, los coeficientes
y
de la ecuación resultante,
, determinan un vector
(vector normal de la recta) que es perpendicular a la recta, en particular: a
en la primera descripción; a
, en la segunda.
- Encuentra la ecuación de la recta que pasa por dos puntos usando álgebra lineal.
- Por cinco puntos distintos del plano pasa una única cónica . Este sencillo principio es una manera escueta de afirmar que con fijar cinco puntos distintos (en posición general), somos capaces de encontrar (determinar los coeficientes de) una ecuación implícita de la forma
, y que cualquier otra es el resultado de multiplicar todos los coeficientes por un factor no nulo. Aunque no entraremos en el concepto general de “puntos en posición general”, basta decir que en este caso quiere decir que los puntos son distintos y que no hay tres que estén alineados.
Este problema, dadas las coordenadas de los cinco puntos, se puede resolver con cálculo matricial. Si 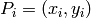 , para
, para 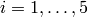 , son cinco puntos distintos, la ecuación buscada, de la forma
, son cinco puntos distintos, la ecuación buscada, de la forma 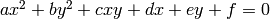 , es verificada por todos ellos, y así se plantean las cinco ecuaciones
, es verificada por todos ellos, y así se plantean las cinco ecuaciones
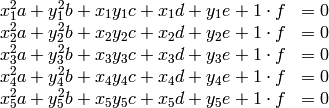
que son lineales en sus incógnitas (los coeficientes  ,
, 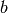 ,
, 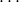 ,
, 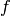 ). Este es un sistema lineal compatible, y si los puntos están en posición general su matriz de coeficientes es de rango
). Este es un sistema lineal compatible, y si los puntos están en posición general su matriz de coeficientes es de rango 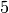 . Si
. Si 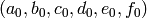 es una solución (no trivial), cualquier otra es de la forma
es una solución (no trivial), cualquier otra es de la forma 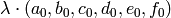 . Pero es obvio que todas estas soluciones nos dan ecuaciones para una misma curva (¿por qué?).
. Pero es obvio que todas estas soluciones nos dan ecuaciones para una misma curva (¿por qué?).
Encuentra la cónica que pasa por cinco puntos en posición general:
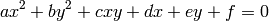
sage: puntos = [(0,0),(0,1),(1,3),(2,1),(1,0)]
sage: var('x y')
sage: coefs = matrix(QQ,5,6)
sage: for j in range(5):
... x0, y0 = puntos[j]
... coefs[j,0] = x0^2 #Primera columna (coef. de a)
... coefs[j,1] = y0^2 #Segunda columna (coef. de b)
... coefs[j,2] = x0*y0 #Tercera columna (coef. de c)
... coefs[j,3] = x0 #Cuarta columna (coef. de d)
... coefs[j,4] = y0 #Quinta columna (coef. de e)
... coefs[j,5] = 1 #Sexta columna (coef. de f)
sage: show(coefs)
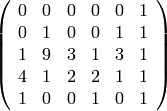
sage: sol = coefs.solve_right(vector([0,0,0,0,0]))
sage: show(sol)
sage: coefs.right_kernel().basis()[0]
(1, 1/2, -1, -1, -1/2, 0)
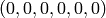
sage: vk = coefs.right_kernel().basis()[0]
sage: a,b,c,d,e,f = vk
sage: curva = a*x^2 + b*y^2 + c*x*y + d*x + e*y + f
sage: show(curva)
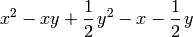
sage: implicit_plot(curva,(x,-1,4),(y,-1,5))+point2d(puntos,color=(1,0,0),pointsize=30)
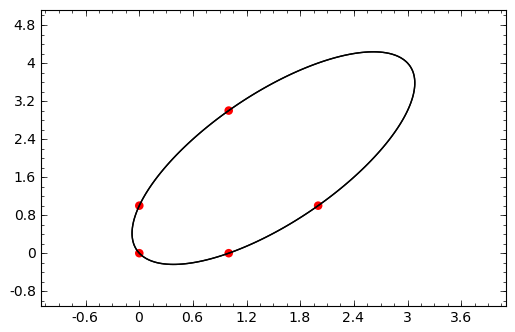
Encuentra 5 puntos tal que la cónica que pasa por ellos sea una hipérbola.
Si fijamos 4 puntos del plano en posición general, encontramos muchas cónicas que pasan por todos los puntos. En este caso, los coeficientes de la ecuación de la cónica que pasa por los 4 puntos deben satisfacer 4 ecuaciones:
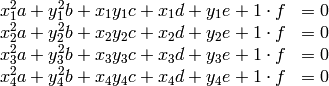
sage: puntos = [(0,0),(0,1),(1,0),(2,2)]
sage: var('x y')
sage: coefs = matrix(QQ,4,6)
sage: for j in range(4):
... x0, y0 = puntos[j]
... coefs[j,0] = x0^2
... coefs[j,1] = y0^2
... coefs[j,2] = x0*y0
... coefs[j,3] = x0
... coefs[j,4] = y0
... coefs[j,5] = 1
sage: show(coefs)
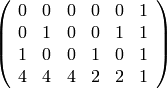
sage: K = coefs.right_kernel()
sage: v1 = K.basis()[0]
sage: v2 = K.basis()[1]
sage: show(K.basis())
![\left[\left(1,0,-\frac{1}{2},-1,0,0\right), \left(0,1,-\frac{1}{2},0,-1,0\right)\right]](_images/math/ec9aade369c0e6ee530c8d73dbaaf7abe75b3e44.png)
Cualquier vector no nulo de K da lugar a una cónica que pasa por los 4 puntos. No todas son equivalentes, aunque por supuesto dos vectores proporcionales dan lugar a la misma curva. Al conjunto de cónicas que pasa por los cuatro puntos lo llamamos el haz de cónicas por los 4 puntos.
sage: c1 = 1
sage: c2 = -3
sage: a,b,c,d,e,f = c1*v1 + c2*v2
sage: curva = a*x^2 + b*y^2 + c*x*y + d*x + e*y + f
sage: grafica = point2d(puntos,color=(1,0,0),pointsize=30) + implicit_plot(curva,(x,-1,4),(y,-1,4))
sage: grafica.show()
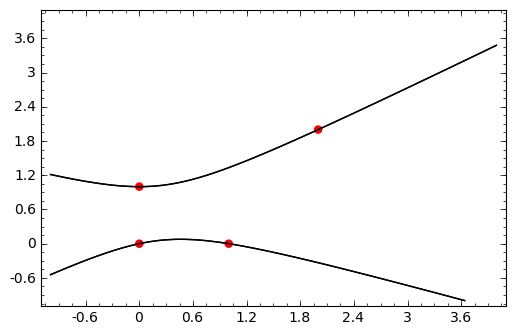
Dibuja varias cónicas del haz en la misma gráfica .