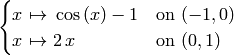El método limit permite calcular límites de funciones. Para calcular el límite de f en el punto x0 .
f.limit(x=x0)
Cuando la función está definida y es continua en el punto, el valor del límite es igual al límite de la función:
sage: var('x')
sage: f1=x^2
sage: f2=(x+1)*sin(x)
sage: f3=f2/f1
sage: f4=sqrt(f3)/(x^2+1)
sage: print f1.limit(x=1)
sage: print f1(x=1)
1
1
Se puede calcular el límite en un punto de la recta, o también en 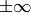 (al que podemos referirnos por \+Infinity o por oo ).
(al que podemos referirnos por \+Infinity o por oo ).
sage: f3.limit(x=0)
+Infinity
sage: f3.limit(x=+oo)
0
Si el límite no existe, la función limit devuelve el valor und , abreviatura de undefined .
sage: f=1/(x*sin(x))
sage: f.show()
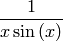
sage: f.limit(x=+Infinity)
und
Usando el argumento adicional ‘ dir ‘, podemos especificar si se trata de un límite lateral, por la derecha (‘right’ ó ‘+’) o por la izquierda (‘left’ ó ‘-‘):
sage: f=1/x
sage: print f.limit(x=0,dir='+')
sage: print f.limit(x=0,dir='-')
+Infinity
-Infinity
También podemos calcular límites de sucesiones de la misma forma. Al fin y al cabo, si la expresión simbólica admite valores reales, el límite de la función que define en infinito es lo mismo que el límite de la sucesión de naturales definido por la misma expresión.
sage: var('k')
sage: limit(k^2/(k+1)^2, k = oo)
1
sage: limit(2^k/factorial(k), k = oo)
0
El comando sum permite calcular la suma de una serie infinita, pero usando una sintaxis distinta de la usada hasta ahora:
sum(expresion, variable, limite_inferior, limite_superior)
sage: sum(1/k^2, k, 1, oo)
1/6*pi^2
Algunos límites, o sumas, no se pueden resolver sin hipótesis adicionales, y es necesario usar assume .
sage: var('k a')
sage: sum(k^a, a, 1, oo)
Is abs(k)-1 positive, negative, or zero?
Traceback (most recent call last):
...
TypeError: Computation failed since Maxima requested additional constraints (try the command 'assume(abs(k)-1>0)' before integral or limit evaluation, for example):
sage: var('k a')
sage: forget()
sage: assume(abs(k)<1)
sage: sum(k^a, a, 0, oo)
-1/(k - 1)
Observamos que informar a Sage de que -1<k<1 en vez de |k|<1, aunque en principio es equivalente (si entendemos que al escribir desigualdades ya no hablamos de números complejos sino reales), no funciona.
Sirva este ejemplo para recordar que los motores de cálculo simbólico hacen lo que pueden, y no siempre dan el resultado esperado. A veces necesitan que le introduzcamos la información de una forma particular, y fallan si la introducimos de una forma equivalente. Es por ello que normalmente usamos las herramientas de cálculo simbólico de forma interactiva.
sage: var('k a')
sage: forget()
sage: assume(k,'real')
sage: assume(-1<k<1)
sage: sum(k^a, a, 0, oo)
Is abs(k)-1 positive, negative, or zero?
Traceback (most recent call last):
...
TypeError: Computation failed since Maxima requested additional constraints (try the command 'assume(abs(k)-1>0)' before integral or limit evaluation, for example):
El método derivative permite calcular derivadas de funciones simbólicas. Las derivadas se obtienen siguiendo metódicamente las reglas de derivación y no suponen ningún problema al ordenador:
sage: sin(x).derivative(x)
cos(x)
sage: f2.derivative(x)
(x + 1)*cos(x) + sin(x)
Si usamos funciones de una sóla variable, podemos omitir la variable por la que estamos derivando.
sage: f2.derivative()
(x + 1)*cos(x) + sin(x)
Las integrales son más complicadas de tratar mediante cálculo simbólico que las derivadas, ya que no existe ningún método que pueda calcular la integral de cualquier función. En realidad, hay muchas funciones elementales (construídas a partir funciones trigonométricas, exponenciales y algebraicas mediante sumas, productos y composición de funciones) cuyas integrales, aunque estén bien definidas, no se pueden expresar en términos de estas mismas funciones. Los ejemplos 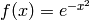 y
y 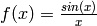 son bien conocidos.
son bien conocidos.
Aunque en teoría existe un algoritmo (el algoritmo de Risch) capaz de decidir si la integral de una función elemental es otra función elemental, dificultades prácticas imposibilitan llevarlo a la práctica, y el resultado es que incluso en casos en los que integramos una función cuya integral es una función elemental, nuestro algoritmo de integración simbólica puede no darse cuenta.
sage: sin(x).integral(x)
-cos(x)
sage: f2=sin(x)
sage: f2.integral(x)
-cos(x)
sage: f5=1/sqrt(1-x^2)
sage: f5.show()
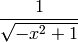
sage: f5.integral(x)
arcsin(x)
Las funciones racionales (cociente de un polinomio por otro polinomio) se pueden integrar de forma exacta, siempre que sea posible descomponer los denominadores en fracciones simples (el algoritmo para integrar funciones racionales es el mismo que estudiásteis en el Bachillerato).
sage: f6=(x^3+4*x^2-x-2)/(x^2+8*x+1)
sage: f6i = f6.integral(x)
sage: f6i.show()
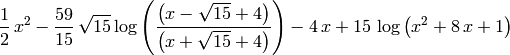
Sin embargo, algunas integrales no se pueden expresar en términos de funciones elementales y sólo se pueden dejar indicadas.
sage: f7=sin(x)/x
sage: f7i=f7.integral(x)
sage: print f7i
sage: f7i.show()
integrate(sin(x)/x, x)
Algunas funciones tienen integrales que se pueden expresar en términos de funciones elementales, pero el ordenador no es capaz de encontrarlas y desiste.
sage: f=(x^10*sin(x^3)*cos(x)).derivative()
sage: print f
3*x^12*cos(x^3)*cos(x) - x^10*sin(x^3)*sin(x) + 10*x^9*sin(x^3)*cos(x)
sage: #Observa que el resultado contiene integrales; esto quiere decir que no ha completado la integracion
sage: #de la funcion f y lo ha dejado indicado
sage: g=f.integral(x)
sage: print g
1/4*x^10*sin(x^3 - x) + 1/4*x^10*sin(x^3 + x) + 1/4*x^10*cos(x^3 - x) - 1/4*x^10*cos(x^3 + x) + 1/4*integrate(-(3*x^12 + x^10 - 10*x^9)*sin(x^3 + x) + (3*x^12 + x^10 + 10*x^9)*cos(x^3 + x), x) + 1/4*integrate((3*x^12 - x^10 - 10*x^9)*cos(x^3 - x) + (3*x^12 - x^10 + 10*x^9)*sin(x^3 - x), x)
Las integrales definidas son también complicadas de calcular de forma exacta. Sin embargo, una integral definida es un número real, y en las aplicaciones es suficiente con aproximar ese número con suficiente precisión.
Si insistimos en hacer el cálculo exacto, podemos usar el mismo método integral , pero pasando además dos argumentos: el extremo inferior y superior del intervalo.
sage: sin(x).integral(0,pi)
2
sage: f(x) = sin(x)
sage: F = f.integral(x)
sage: v = F(x=pi) - F(x=0)
sage: print v
sage: print f.integral(x,0,pi)
2
x |--> 2
sage: #Algunas integrales definidas no se pueden calcular de forma exacta,
sage: #y las deja indicadas
sage: f7=sin(x)/x
sage: integral(f7,x,0,1)
integrate(sin(x)/x, x, 0, 1)
Sin embargo, todas las integrales definidas se pueden calcular de forma aproximada con la función numerical_integral , que acepta como argumentos la función a integrar y los extremos del intervalo, pero devuelve una tupla formada por el valor aproximado de la integral y una cota del error cometido.
sage: numerical_integral(f7,0,1)
(0.94608307036718298, 1.0503632079297087e-14)
sage: numerical_integral?
<html>...</html>
Las funciones de una variable simbólica también se pueden integrar con el método nintegral, que además del valor aproximado de la integral y una estimación del error devuelve dos parámetros adicionales.
sage: f7.nintegral(x,0,1)
(0.94608307036718309, 1.050363207929709e-14, 21, 0)
Lee la ayuda del método nintegral , y realiza llamadas a nintegral tales que:
- el último valor devuelto por nintegral sea positivo
- el tercer valor devuelto por nintegral sea mayor que 100
sage: f7.nintegral?
<html>...</html>
Vamos a manejar varios comandos para hacer gráficas:
- plot(f) (ó f.plot() ) dibujan la función f.
- point2d(lista) , dibuja los puntos de la lista que se pasa como argumento.
- line2d(lista) , dibuja líneas entre los puntos de la lista que se pasa como argumento.
sage: plot(f2)
sage: puntos = [(0,0),(1,1),(2,0),(3,1)]
sage: point2d(puntos)
sage: line2d(puntos)
Además de los argumentos obligatorios, le podemos pasar argumentos opcionales. Los siguientes parámetros son bastante útiles:
- plot(f,xmin,xmax) muestra la función entre los puntos xmin y xmax .
- point2d(puntos, pointsize=20) permite especificar el tamaño de los puntos
- line2d(puntos, thickness= 2) permite especificar el grueso de la línea
- plot(f, color=(1,0,0)) permite especificar el color como una tupla de 3 valores: los tonos de rojo, verde y azul.
- point2d(puntos, rgbcolor=(1,0,0) ) y line2d(puntos, rgbcolor=(1,0,0) ) permiten especificar el color como una tupla de 3 valores: los tonos de rojo, verde y azul.
sage: plot(f2,-5,5,color=(1,0,0))
sage: point2d(puntos, pointsize=30)
sage: line2d(puntos, thickness= 3, color=(0,1,0))
Las gráficas se pueden almacenar en variables.
sage: grafica1 = plot(sin(x),-pi,pi)
sage: grafica2 = point((0,0), pointsize=30, rgbcolor=(1,0,0) )
sage: grafica3 = line([(-pi,-pi),(pi,pi) ], rgbcolor=(0,1,0) )
Las gráficas tienen un tipo de datos especial, con sus propios métodos.
sage: grafica1?
<html>...</html>
sage: grafica1.
Traceback (most recent call last):
...
SyntaxError: invalid syntax
El operador suma (+) permite combinar gráficas en una sóla imagen.
sage: grafica = grafica1+grafica2+grafica3
sage: grafica.show()
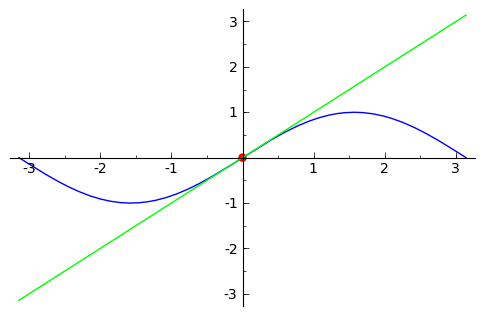
Podemos combinar muchas gráficas en una sóla almacenando las gráficas en una lista, y luego usando la función sum .
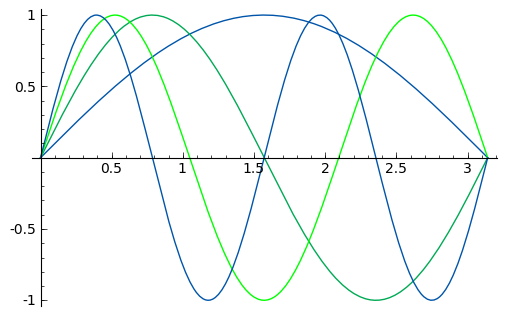
sage: lista = [plot(sin(n*x), (0, pi), color=(0,n/3,1-n/3)) for n in [1..4]]
sage: grafica = sum(lista)
sage: grafica.show()
Algunos problemas típicos del cálculo no se prestan tan bien al cálculo simbólico como los límites y las derivadas. Un ejemplo típico es encontrar los puntos donde una función toma el valor 0. Podemos intentar resolver la ecuación f=0 usando el comando solve , al que pasamos como argumento la variable simbólica para la que queremos resolver.
f = x^2 - 3
f.solve(x)
> [x == -sqrt(3), x == sqrt(3)]
Aunque el resultado es adecuado en muchos casos particulares importantes, francamente pocas ecuaciones que podamos definir combinando más de una función elemental tienen raíces que se puedan escribir de forma exacta como una expresión simbólica. Además, tenemos el problema de la multiplicidad de raíces y extremos de las funciones.
La solución que nos ofrece SAGE es buscar las raíces de forma numérica en un intervalo dado. Una llamada al método find_root :
f.find_root(a,b)
nos devuelve una raíz de la función f en el intervalo [a,b] , y lanza un error si la función no tiene ceros en ese intervalo.
sage: f6 = x^2 - 3
sage: f6.solve(x)
[x == -sqrt(3), x == sqrt(3)]
sage: f7=2*x+sin(x)-2
sage: #El resultado de llamar a solve no es satisfactorio
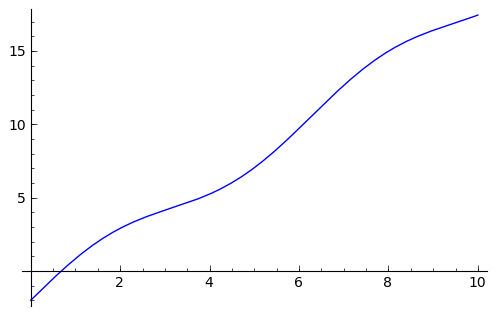
sage: f7.solve(x)
[x == -1/2*sin(x) + 1]
sage: f7.plot(0,10)
sage: f7.find_root(0,2)
0.68403665667799907
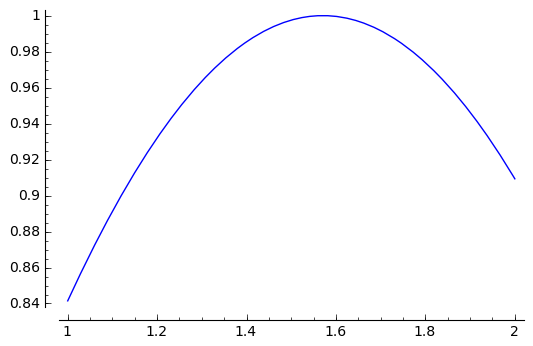
sage: sin(x).find_root(1,2)
Traceback (most recent call last):
...
RuntimeError: f appears to have no zero on the interval
sage: plot(sin(x),1,2)
Si la función tiene más de una raíz en el intervalo, find_root devuelve una cualquiera de las raices.
sage: sin(x).find_root(1,30)
21.991148575128552
Las funciones find_minimum_on_interval y find_maximum_on_interval funcionan de forma similar a find_root :
f.find_minimum_on_interval(a,b)
devuelve una tupla con dos valores: el minimo de la función en el intervalo y el punto donde se alcanza.
sage: f8 = x^2 - 3*sin(x)
sage: plot(f8,-4,4)
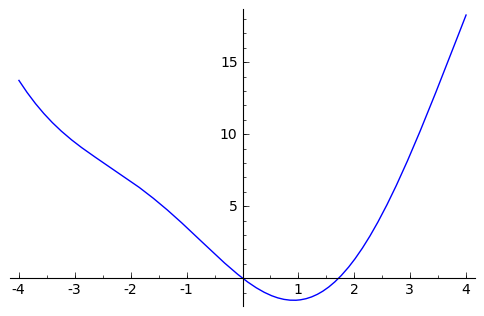
sage: (y0,x0) = f8.find_minimum_on_interval(-4,4)
sage: print x0,y0
sage: grafica = plot(f8,-4,4) + point2d((x0,y0), pointsize=30, rgbcolor=(1,0,0))
sage: grafica.show()
0.914856478862 -1.54046280571
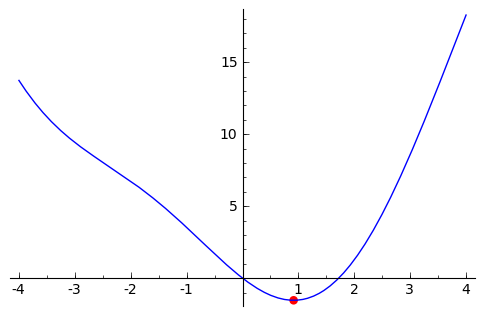
En realidad, el valor devuelto por find_minimum_on_interval es uno cualquiera de los mínimos locales de la función. En la documentación de la función leemos que usa el método de Brent : “una combinación del método de bisección, el método de la secante y el método de interpolación cuadrática”:
Todos estos métodos pueden detenerse en un extremo local, y el algoritmo de Brent también. En general, el problema de encontrar máximos globales no es trivial, aunque para funciones de una variable de las que se conoce alguna propiedad extra no es difícil encontrar procedimientos para encontrar los extremos.
sage: f8.find_minimum_on_interval?
<html>...</html>
sage: f9=sin(x/10)+sin(x)
sage: plot(f9,0,50)
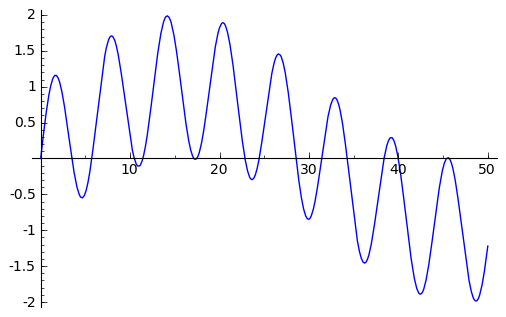
sage: f9.find_maximum_on_interval(10,20)
(1.987809504903955, 14.152658043591082)
sage: f9.find_maximum_on_interval(0,50)
(1.8920281240458212, 20.37533953333153)
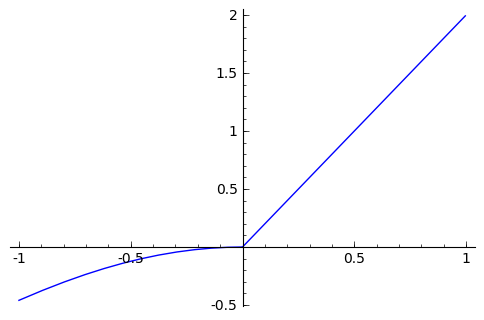
Usando la función Piecewise podemos construir funciones definidas a trozos. Para ello, pasamos a la función Piecewise una lista de tuplas, donde cada tupla contiene un intervalo y una función. El resultado es la función definida a trozos que vale en cada intervalo la función que hemos pasado.
f = Piecewise( [(I1, f1), (I2,f2), ...] )
Pasamos los intervalos como tuplas con los extremos del intervalo.
sage: f1=sin(x)-x
sage: f2=x^2
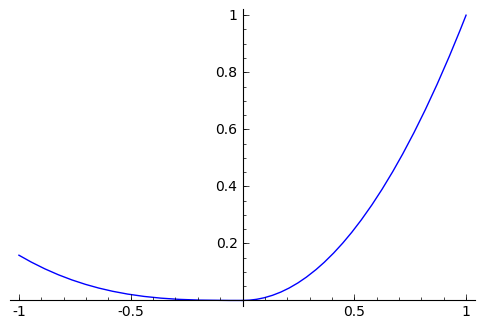
sage: f=Piecewise([((-1,0),f1),((0,1),f2)])
sage: show(f)
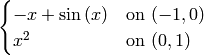
sage: plot(f)
sage: fp = f.derivative(x)
sage: show(fp)
sage: plot(fp)