Navegación

Ejercicios

1.

Queremos encontrar todos los triángulos equilateros con vértices en tres rectas paralelas dadas.

  • Plantea el problema usando variables simbólicas de la forma más directa posible, usando la definición de triángulo equilátero: los tres lados deben ser iguales, y observa como Sage falla miserablemente.
  • Mastica un poco el problema, usando algunas de las sugerencias siguientes:
  • Evita las raices cuadradas que tienen varias soluciones.
  • Fija la primera recta al eje de las x.
  • Fija el primer vértice del triángulo al origen de coordenadas.
  • Usa una definición alternativa de triángulo equilátero: la rotación de ángulo 60º con vértice p1 lleva p2 a p3.

2.

  • Calcula el centro y el radio de la circunferencia que pasa por tres puntos del plano, de coordenadas (x1,y1), (x2,y2) y (x3,y3).
  • Intenta entender la fórmula obtenida para el radio del círculo, en función de conceptos geométricos intrínsecos como áreas, distancias y ángulos.

3.

Un teorema de álgebra afirma que todo polinomio simétrico 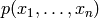p(x_1,\dots, x_n) se puede expresar en función de los polinomios simétricos elementales:

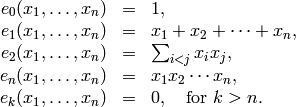
\begin{array}{rcl} e_0(x_1,\ldots,x_n) &=& 1,\\ e_1(x_1,\ldots,x_n) &=& x_1+x_2+\cdots+x_n,\\ e_2(x_1,\ldots,x_n) &=& \textstyle\sum_{i<j}x_ix_j,\\ e_n(x_1,\ldots,x_n) &=& x_1x_2\cdots x_n,\\ e_k(x_1,\ldots,x_n) &=& 0, \quad{\rm for}\ k>n.\\ \end{array}

Por ejemplo:

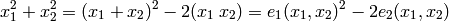
x_1^2 + x_2^2 = (x_1 + x_2)^2 - 2(x_1\:x_2) = e_1(x_1,x_2)^2 - 2 e_2(x_1,x_2)

  • Busca a mano una forma de expresar el polinomio x_1^2+x_2^2+ x_3^2+x_4^2 en función de los polinomios simétricos elementales en cuatro variables.
  • Busca a mano una forma de expresar el polinomio x_1^3+x_2^3 en función de los (tres) polinomios simétricos elementales en dos variables.
  • Busca a mano una forma de expresar el polinomio -\frac{1}{6} \, x_{1}^{3} - \frac{1}{2} \, x_{1}^{2} x_{2} - \frac{1}{2}\, x_{1} x_{2}^{2} - \frac{1}{6} \, x_{2}^{3} + x_{1} + x_{2} en función de los (tres) polinomios simétricos elementales en dos variables.
  • Busca a mano una forma de expresar el polinomio de Taylor de grado k de sin(x_1+x_2) en función de los (tres) polinomios simétricos elementales en dos variables (indicación: busca un método para calcular el polinomio de Taylor)

4: Trabajar con un número arbitrario de variables simbólicas

El código siguiente:

N = 5
var(','.join(['x%d'%j for j in range(1, N+1)]))

define las N variables simbólicas x1,...,xN.

Si además guardas las variables en una lista, puedes iterar la lista de variables para, por ejemplo, multiplicarlas todas:

N = 5
vs = var(','.join(['x%d'%j for j in range(1, N+1)]))
p = 1
for v in vs:
    p = p\*v
print p
  • Escribe una función que, dados dos números n y k , construya el polinomio p_k(x_1,\ldots,x_n)=\sum\nolimits_{i=1}^nx_i^k = x_1^k+\cdots+x_n^k
  • Escribe una función que, dado un número k , construya el polinomio simétrico en k variables: e_k:

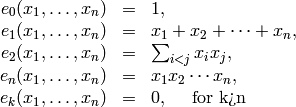
\begin{array}{rcl} e_0(x_1,\ldots,x_n) &=& 1,\\ e_1(x_1,\ldots,x_n) &=& x_1+x_2+\cdots+x_n,\\ e_2(x_1,\ldots,x_n) &=& \textstyle\sum_{i<j}x_ix_j,\\ e_n(x_1,\ldots,x_n) &=& x_1x_2\cdots x_n,\\ e_k(x_1,\ldots,x_n) &=& 0, \quad \text{ for k>n} \end{array}

  • Escribe código que compruebe las identidades de Newton , para k desde 2 hasta 5 ( más información ):

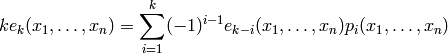
ke_k(x_1,\ldots,x_n) = \sum_{i=1}^k(-1)^{i-1} e_{k-i} (x_1,\ldots,x_n) p_i(x_1,\ldots,x_n)

sage: N = 5
sage: var(','.join(['x%d'%j for j in range(1, N+1)]))
(x1, x2, x3, x4, x5)

sage: N = 5
sage: vs = var(','.join(['x%d'%j for j in range(1, N+1)]))
sage: p = 1
sage: for v in vs:
...       p = p*v
sage: print p
x1*x2*x3*x4*x5

5.

  • Escribe código que componga la matriz de van der Monde n x n:

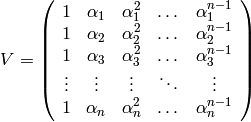
V=\left(\begin{array}{ccccc} 1 & \alpha_1 & \alpha_1^2 & \dots & \alpha_1^{n-1}\\ 1 & \alpha_2 & \alpha_2^2 & \dots & \alpha_2^{n-1}\\ 1 & \alpha_3 & \alpha_3^2 & \dots & \alpha_3^{n-1}\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & \alpha_n & \alpha_n^2 & \dots & \alpha_n^{n-1} \end{array}\right)

  • Demuestra que la matriz de van der Monde es invertible si los números \alpha_1,\dots,\alpha_n son distintos, para n=2,3 y 4. (Indicación: factoriza el determinante)

Contenidos

Tema anterior

Cálculo simbólico

Próximo tema

Cálculo diferencial en una variable

Esta página

Navegación

© Copyright 2005--2011, The Sage Development Team. Creado con Sphinx 1.1.2.