Una función recursiva es aquella que contiene en el bloque de instrucciones que la definen una llamada a la propia función. En matemáticas también se usan definiciones recursivas y, tanto en un caso como en otro, hay que tener cuidado para estar seguro de que la definición es consistente:
- La función debe poder calcularse directamente en uno o más de los posibles casos de uso. Estos casos se llaman casos base.
- La llamada a la función con unos argumentos que no son casos base debe depender del valor de la función en otros argumentos distintos, que deben estar más cercanos a los casos base en algún sentido. Esta regla no es muy precisa, pero no se puede dar una receta general, como veremos.
Como ejemplo, escribimos una implementación recursiva de la función factorial, que se basa en la definición recursiva:
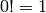
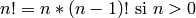
sage: def factorial_rec(n):
... '''Devuelve el factorial de un numero, usando llamadas recursivas
... '''
... if n == 0:
... return 1
... else:
... return n*factorial_rec(n-1)
sage: var = factorial_rec(1)
Como vemos, la implementación recursiva es una traslación bastante literal de la definición matemática del factorial.
Al igual que un bucle while mal diseñado puede repetirse infinitamente, una función recursiva mal diseñada puede repetirse indefinidamente.
sage: def fun_rec_inf(n):
... '''Funcion recursiva desastrosa
... '''
... return n+fun_rec_inf(n-1) #Nos hemos olvidado el caso base
sage: fun_rec_inf(10)
WARNING: Output truncated!
<html>...</html>
RuntimeError: maximum recursion depth exceeded
En realidad la ejecución se detiene sola sin necesidad de que interrumpamos el cálculo. En python , el lenguaje que usa Sage, hay un límite a la cantidad de veces que una función recursiva puede llamarse a sí misma (en general está fijado en 1000 llamadas recursivas).
En python, las funciones son ciudadanos de primera clase, lo que significa que podemos guardar funciones en variables normales, guardarlas en listas, pasarlas como argumentos a otras funciones, etcétera.
sage: funcion = factorial
sage: funcion(4)
24
sage: funciones = [is_prime, is_prime_power, is_power_of_two, is_square]
sage: k = 5
sage: for f in funciones:
... print f(k)
True
True
False
False
Poder pasar funciones como argumentos a otras funciones permite abstraer algunos patrones usuales, y escribir código genérico que realiza las operaciones para funciones arbitrarias. De este modo la reutilización de código aumenta sensiblemente.
Como ejemplo, escribimos una función genérica que, partiendo de un valor inicial, itera una condición hasta que una cierta propiedad se verifique:
sage: def itera_hasta(f, p, ini):
... '''Itera la funcion f, comenzando por el valor inicial ini,
... hasta que se verifique la condicion p
...
... Devuelve el elemento final de la iteracion
... '''
... t = ini
... while not p(t):
... t = f(t)
... return t
Usando esta función genérica, podemos calcular raices cuadradas con el algoritmo de Herón:
sage: a = 2.0
sage: epsilon = 1e-5
sage: def f(t):
... return (1/2)*( t + a/t)
...
sage: def p(t):
... return abs(t^2 - a) < epsilon
...
sage: print itera_hasta(f, p, 2)
1.41421568627451
Pero también podemos aproximar ceros de funciones usando el método de bisección...
sage: a = 0.0
sage: b = 1.0
sage: def f(t):
... return t^3 + t - 1
sage: epsilon = 1e-5
sage: valor_inicial = (a,b)
sage: def siguiente(t):
... x0, x1 = t
... x_medio = (x0 + x1)/2
... if f(x0)*f(x_medio)<0:
... return (x0, x_medio)
... else:
... return (x_medio, x1)
...
sage: def p(t):
... x0, x1 = t
... return abs(f(x0)) + abs(f(x1)) < epsilon
...
sage: print itera_hasta(siguiente, p, valor_inicial)
(0.682327270507812, 0.682331085205078)
El siguiente ejemplo es un clásico: tomamos una lista y la “reducimos” usando una función que toma dos elementos y devuelve uno (como por ejemplo, la suma) . Para ello, aplicamos la funcion entre cada dos elementos de la lista. El primer ejemplo con ‘+’ no funciona, lo ponemos sólo a modo de ejemplo.
lista : [ x1, x2, x3, x4, x5 ]
reduce(+, lista) : x1 + x2 + x3 + x4 + x5
reduce(f, lista) : f(f(f(f(x1, x2), x3), x4), x5)
sage: def reducir(operacion, lista):
... acumulador = lista[0]
... for elemento in lista[1:]:
... acumulador = operacion(acumulador, elemento)
... return acumulador
sage: def concatena_dos_listas(x,y):
... return x+y
sage: reducir(concatena_dos_listas, [range(2),range(7),range(3)])
[0, 1, 0, 1, 2, 3, 4, 5, 6, 0, 1, 2]
En este caso, el patrón es tan común que python ya tiene su propia función reduce , similar a la que hemos definido nosotras.
sage: reduce?
<html>...</html>
A continuación aprenderemos otro estilo de programación en el que visualizamos series de datos (por ejemplo, números) pasando por cajas que los transforman, los filtran o los acumulan de modo que podamos realizar el cálculo deseado partiendo de series de datos conocidas.
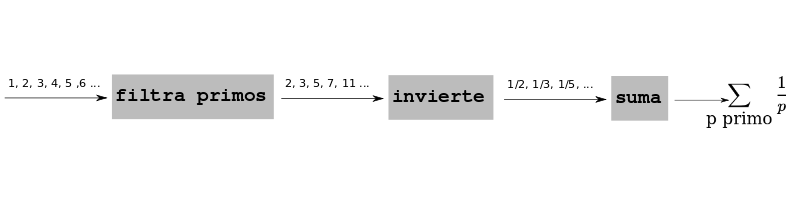
En python existe una sintaxis especial para generar nuevas listas a partir de otras, aplicando una transformación a cada elemento, y seleccionando aquellos elementos que verifican una propiedad.
La instrucción
[f(x) for x in lista_original]
genera una nueva lista, cuyos elementos son el resultado de ejecutar la función f sobre cada elemento de la lista_original .
sage: lista_original = range(10)
sage: print lista_original
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
sage: [x^2 for x in lista_original]
[0, 1, 4, 9, 16, 25, 36, 49, 64, 81]
sage: [exp(-x)+1 for x in lista_original]
[2, e^(-1) + 1, e^(-2) + 1, e^(-3) + 1, e^(-4) + 1, e^(-5) + 1, e^(-6) + 1, e^(-7) + 1, e^(-8) + 1, e^(-9) + 1]
Podemos transformar una lista con datos de un tipo cualquiera (enteros, booleanos, tuplas, cadenas de caracteres) en una lista con datos de cualquier otro tipo.
sage: print lista_original
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
sage: [is_prime(x) for x in lista_original]
[False, False, True, True, False, True, False, True, False, False]
sage: [(sin(x*2*pi/8), cos(x*2*pi/8)) for x in srange(8)]
[(0, 1), (1/2*sqrt(2), 1/2*sqrt(2)), (1, 0), (1/2*sqrt(2), -1/2*sqrt(2)), (0, -1), (-1/2*sqrt(2), -1/2*sqrt(2)), (-1, 0), (-1/2*sqrt(2), 1/2*sqrt(2))]
sage: palabras=['En', 'un', 'lugar', 'de', 'la', 'Mancha', 'de', 'cuyo', 'nombre', 'no', 'quiero', 'acordarme']
sage: [len(palabra) for palabra in palabras]
[2, 2, 5, 2, 2, 6, 2, 4, 6, 2, 6, 9]
sage: [palabra.upper() for palabra in palabras] #El metodo upper() pasa una cadena a mayusculas
['EN', 'UN', 'LUGAR', 'DE', 'LA', 'MANCHA', 'DE', 'CUYO', 'NOMBRE', 'NO', 'QUIERO', 'ACORDARME']
Con la instrucción
[x for x in lista if condicion(x)]
podemos seleccionar sólo aquellos elementos de la lista que verifican una condición. La condición es cualquier expresión o cualquier función que, para un valor x cualquiera, devuelva un valor booleano ( True o False ).
sage: [x for x in lista_original if is_prime(x)]
[2, 3, 5, 7]
sage: [x^2 for x in lista_original if x%2==1]
[1, 9, 25, 49, 81]
sage: [palabra for palabra in palabras if len(palabra)==2]
['En', 'un', 'de', 'la', 'de', 'no']
También podemos combinar ambas técnicas, o incluso recorrer todas las combinaciones de elementos de dos listas distintas:
[funcion(x) for x in lista if condicion(x)]
[funcion(x,y) for x in lista1 for y in lista2]
...
sage: #Todas las sumas de dos numeros menores que k
sage: k = 10
sage: numeros = range(k)
sage: sumas = [x + y for x in numeros for y in numeros]
sage: print sumas
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18]
Pero lo mejor es encadenar varias de estas transformaciones:
sage: k = 10
sage: #Todos los numeros primos menores que k
sage: primos = [x for x in range(k) if is_prime(x)]
sage: #Todas las sumas de dos numeros primos menores que k
sage: sumas_primos = [x + y for x in primos for y in primos]
sage: #Aquellas sumas de dos numeros primos menores que k que son cuadrados perfectos
sage: cuadrados = [x for x in sumas_primos if is_square(x)]
sage: cuadrados
[4, 9, 9]
Las siguientes funciones encapsulan las tareas más usuales que realizamos con listas:
- len(lista) : devuelve la longitud de la lista
- max(lista) : devuelve el máximo de la lista
- min(lista) : devuelve el mínimo de la lista
- sum(lista) : devuelve la suma de los elementos de la lista
- all(lista) : si lista está compuesta de booleanos, devuelve True si todos son ciertos, y False en otro caso.
- any(lista) : si lista está compuesta de booleanos, devuelve True si alguno es cierto, y False en otro caso.
sage: print len([2,4,1,3])
sage: print max([2,4,1,3])
sage: print min([2,4,1,3])
sage: print sum([2,4,1,3])
sage: print all([True, False, False])
sage: print any([True, False, False])
4
4
1
10
False
True
sage: k = 86
sage: divisores = k.divisors() #lista con los divisores de k
sage: print divisores
sage: print sum(divisores) #La suma de los divisores de k
sage: print max(divisores) #El mayor divisor de k
[1, 2, 43, 86]
132
86
Combinadas con las dos técnicas de arriba, estas funciones permiten resolver problemas no triviales:
sage: k = 86
sage: divisores = k.divisors()
sage: #El mayor divisor de k (sin contar a k)
sage: print max([j for j in divisores if j<k])
43
sage: #Son primos todos los divisores de k?
sage: print all([is_prime(j) for j in divisores])
False
sage: #Son primos todos los divisores de k (sin contar 1 ni k)?
sage: print all([is_prime(j) for j in divisores if 1<j<k])
True
Ejercicio. Responde a las siguientes preguntas con las técnicas usadas en esta sesión:
- ¿Cuántos divisores de k=21000 son cuadrados perfectos?
- ¿Hay algún número k entre 20 y 100 tal que 2^k +1 es primo?
- Encuentra el tercer cuadrado perfecto n=k^2 tal que n+1 es primo.
Ejercicio : Escribe otra implementación de la función sumaprimos de la sesión anterior usando estas ideas.
Quizá a estas alturas te hayas dado cuenta de que usar este enfoque indiscriminadamente puede llevar a realizar una cantidad de cálculos desproporcionada y a usar una gran cantidad de memoria, aún cuando el problema no lo necesita. Por ejemplo, para calcular el segundo primo entre 10000 y 100000 podemos hacer:
ls = srange(10000,100000)
primos = [t for t in ls if is_prime(t) ]
print primos[1]
pero esto nos obliga a guardar en memoria todos los números naturales entre 10000 y 100000, y después a calcular si cada uno es primo, sólo para quedarnos con el segundo.
sage: %time
sage: ls = srange(10000,100000)
sage: primos = [t for t in ls if is_prime(t) ]
sage: print primos[2]
10037
CPU time: 0.39 s, Wall time: 0.39 s
Sin embargo, es posible mantener esta sintaxis sin hacer cálculos innecesarios. Para ello, usamos generadores , objetos que generan los elementos de la lista uno por uno, según se vayan solicitando desde otras partes del programa. A esta técnica se le denomina evaluación perezosa , porque no se hacen cálculos hasta que no son necesarios.
Por ejemplo, la función xsrange es la versión perezosa de srange (con la misma sintaxis). Mientras que srange(100) inmediatamente calcula los enteros menores que 100 y los guarda en una lista, xsrange(100) devuelve un generador, que no calcula los números en ese momento:
sage: srange(100)
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99]
sage: xsrange(100)
<generator object generic_xsrange at 0x5dacf50>
Una vez creado el generador, podemos pedir los números uno por uno, usando el método next() , o recorrerlos todos, usando un bucle for igual que si fuera una lista:
sage: xlista = xsrange(100)
sage: print xlista.next()
sage: print xlista.next()
0
1
sage: acumulador = 0
sage: for j in xsrange(101):
... acumulador += j
sage: print acumulador
5050
Podemos escribir nuestros propios generadores usando una notación similar a la de transformaciones de listas, sólo que poniendo paréntesis alrededor de nuestra expresión en vez de corchetes:
generador = (expresion for x in secuencia if condicion)
sage: genera_cuadrados = (x^2 for x in xsrange(10))
sage: for c in genera_cuadrados:
... print c
0
1
4
9
16
25
36
49
64
81
Ahora podemos modificar el programa original para calcular el segundo primo entre 10000 y 100000, usando una cantidad de memoria y cpu equivalente a un programa tradicional:
sage: %time
sage: ls = xrange(10000,100000)
sage: primos = (t for t in ls if is_prime(t) )
sage: primos.next()
sage: print primos.next()
10009
CPU time: 0.01 s, Wall time: 0.01 s
sage: %time
sage: contador = 2
sage: for j in xsrange(10000,100000):
... if is_prime(j):
... contador -= 1
... if contador == 0:
... break
sage: print j
10009
CPU time: 0.00 s, Wall time: 0.00 s
Sigamos la ejecución del programa paso a paso:
ls = xrange(10000,100000)
primos = (t for t in ls if is_prime(t) )
con estas dos líneas, definimos dos generadores, pero no se realiza ningún cálculo.
primos.next()
al llamar al método next , ponemos a trabajar al generador primos , que debe rodar hasta devolver un número primo. Para ello, prueba los números de la lista ls uno por uno. Cuando encuentra uno que pasa el filtro is_prime(t) , lo devuelve. En la primera llamada a next , primos devuelve el número 10007, el primer primo mayor que 10000.
print primos.next()
pedimos otro número más a primos , que pide a su vez números al generador ls continuando donde lo dejó. Recorre primero el número 10008 e inmediatemente después encuentra 10009, que es primo. El programa concluye.
Por supuesto, es interesante combinar los generadores con el enfoque de flujos que tratamos hoy. Consideremos por ejemplo la pregunta:
¿Hay algún número k entre 1000 y 10000 tal que 2*k +1 es primo?
Para comprobar la pregunta, podemos comprobar si el número 2*k+1 es primo para cada valor de k. Por supuesto, en cuanto encontremos un valor de k para el que 2*k+1 es primo podemos parar, y responder a la pregunta con un sí .
Un enfoque tradicional se aprovecha de esta propiedad:
hay_alguno = False
for k in srange(1000,10000):
if is_prime(2*k+1):
hay_alguno = True
break
print hay_alguno
mientras que si transformamos listas de forma naive, tendremos que comprobar si todos los números son primos:
any([is_prime(2*k+1) for k in srange(1000,10000)])
Pero basta usar un generador para volver a conseguir un programa eficiente:
any(is_prime(2*k+1) for k in xsrange(1000,10000))
Observa que, como el generador ya estaba entre parentésis, no necesitamos poner dobles paréntesis.
sage: %time
sage: hay_alguno = False
sage: for k in srange(1000,10000):
... if is_prime(2*k+1):
... hay_alguno = True
... break
sage: print hay_alguno
True
CPU time: 0.01 s, Wall time: 0.00 s
sage: %time
sage: any([is_prime(2*k+1) for k in srange(1000,10000)])
True
CPU time: 0.05 s, Wall time: 0.05 s
sage: %time
sage: any(is_prime(2*k+1) for k in srange(1000,10000))
True
CPU time: 0.01 s, Wall time: 0.00 s
sage: %time
sage: any(is_prime(2*k+1) for k in xsrange(1000,10000))
True
CPU time: 0.00 s, Wall time: 0.00 s
Escribir generadores en una línea a veces es poco práctico. Más importante es que en los generadores de una línea no se guarda ninguna variable de estado entre cada par de iteraciones. Por ejemplo, podemos calcular los distintos bits de un número entero usando la fórmula para el bit j-ésimo: “divide por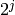 
y toma el resto de dividir por 2”:
sage: def bit_j_esimo(a, j):
... return (a//2^j)%2 # a//b calcula el cociente de la división entera
... #de dividir a entre b
sage: a = 19
sage: print list( bit_j_esimo(a,j) for j in range(0, int(log(a)/log(2)) + 1) )
sage: print sum( bit_j_esimo(a,j) for j in range(0, int(log(a)/log(2)) + 1) )
[1, 1, 0, 0, 1]
3
Sin embargo, es más claro calcular los bits uno por uno haciendo una división por dos cada vez. La sintaxis para los generadores es la misma que para funciones, sólo que usando la instrucción
yield x
para devolver un valor. El objeto creado no es una función, sino un generador, que devuelve potencialmente varios valores, según los soliciten al generador. Cada vez que pedimos un elemento nuevo al generador, el flujo del programa avanza dentro del código de la función hasta que se encuentra con un yield, y entonces devuelve ese valor y se queda congelado hasta que le vuelvan a pedir otro valor:
def bits(a):
while a:
yield a%2
a = a//2
Más información sobre generadores:
sage: def bits(a):
... while a:
... yield a%2
... a = a//2
sage: list(bits(19))
[1, 1, 0, 0, 1]
sage: g = bits(123)
sage: print g.next()
sage: print g.next()
sage: print g.next()
1
1
0
sage: g = bits(2)
sage: print g.next()
sage: print g.next()
sage: print g.next()
0
1
Traceback (most recent call last):
...
StopIteration