Guarda en variables los coeficientes de polinomio de segundo orden. Escribe un código que muestra por pantalla información sobre las raíces del polinomio (tiene dos raíces distintas, una doble, o ninguna).
Para la lista de números de abajo:
- Escribe un bucle for que escriba el resto de dividir cada uno de ellos por 5
- Escribe un bloque for con un bloque if anidado que escriba sólo los múltiplos de 3.
- Escribe un bloque for con otro bloque for anidado que, para cada uno de esos números, escriba, en una misma línea, todos sus divisores (es decir, no uses el método divisors ).
sage: numeros = [1, 3, 7, 13, 21, 31, 43, 57, 73, 91]
Escribe un bucle while que sume los inversos de los números naturales 1/k hasta que la suma sea mayor que 10. Escribe el número k en el que la suma se detiene.
En este ejercicio, utilizamos un algoritmo que aproxima la raíz cuadrada de un número real positivo a . El algoritmo es iterativo: comienza con una aproximación burda:
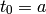
y después en cada iteración del algoritmo sustituimos t por otra aproximación mejor:
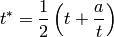
Este algoritmo para calcular raíces cuadradas era conocido por los babilonios, y a veces se le llama algoritmo de Herón . La sucesión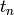 
converge a la raiz de a.
- Escribe una función que acepte dos argumentos: un número real a y un error máximo
, y devuelva una aproximación b al número
con error menor que el error máximo
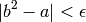
Busca un número natural k tal que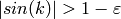 
. No pruebes valores de 
demasiado pequeños: algo así como 0.01 es razonable. Para valores más pequeños, k puede ser muy grande.
Definimos una secuencia de números por la siguiente regla: el número siguiente a n es n/2 si n es par, y 3n+1 si n es impar.
- Escribe una función que acepte como argumento un número k , y escriba por pantalla todos los números de la secuencia comenzando por k hasta y parando cuando se alcance por primera vez el número 1.
- Escribe una función que acepte como argumento un número k , y devuelva el número de veces que se ha iterado la regla anterior hasta llegar a 1 partiendo de k.
- Aprovecha la función del apartado anterior para encontrar un número tal que la secuencia tarde al menos 50 pasos en alcanzar 1.
Nota: Se ha conjeturado, pero no se ha demostrado todavía, que la secuencia siempre alcanza 1 eventualmente: