En todo modelo matemático debemos seleccionar las características del problema que nos interesa estudiar, y descartar toda aquella información que hace el análisis más complicado pero no es esencial.
En este caso, pretendemos estudiar los trucos que son posibles desde un punto combinatorio, es decir, que descartamos variables continuas como la fuerza con la que se debe lanzar cada objeto, su tiempo de vuelo o la altura que alcanza, y nos fijamos sólamente en información discreta.
Como primer paso, dividimos el tiempo en instantes de igual longitud (y a cada instante lo llamamos un beat, o un pulso). A continuación, anotamos qué hacemos en cada pulso. Cada vez que lanzamos un objeto, anotamos dentro de cuántos pulsos lo volveremos a lanzar. Si en un instante no lanzamos ningún objeto, anotamos un cero.
De esta forma, toda la complejidad del movimiento del malabarista queda reducida a una secuencia de numéros enteros: 3535004130... A cada uno de los números de la secuencia, lo llamamos la altura, porque cuando lanzamos un objeto más alto, tarda más tiempo en caer. Sin embargo, no es una altura medida en metros ni en ninguna otra unidad de medida, ya que para si para que un objeto caiga dentro de 1 instante necesitamos lanzarlo a una altura h, para que caiga dentro de k instantes necesitaremos lanzarlo a altura h*k^2.
Si observamos a los malabaristas ejecutar varios trucos clásicos, encontraremos que las secuencias de números a que dan lugar son periódicas:
Aunque si le pedimos al malabarista que comience con una cascada y cambie a una “shower”, encontraremos la secuencia ..33341515... y viceversa, si comienza con una “shower” y cambia a una casacada, encontramos ..1515152333...
¿Qué secuencias podemos encontrar? Si asumimos que en cada instante el malabarista puede hacer a lo sumo una acción (e.g., recoger una bola y volverla a lanzar, pero no recoger dos bolas ni lanzar dos bolas), entonces cualquier secuencia que contenga un 4 seguido de un 3 es inviable, porque 4 instantes después del primer lanzamiento, el malabarista recibiría a la vez dos bolas, a las que no podría atender.
Para completar nuestra imagen mental, visualizamos un malabarista haciendo trucos con las dos manos, usando la mano izquierda y la derecha alternativamente, de modo que en los instantes impares usa la mano izquierda y en los pares la derecha.
Nos preguntamos cuáles son las secuencias de números que corresponden a trucos de malabares válidos.
Si estudiamos sólamente patrones periódicos, nos encontramos con la teoría del Site Swap. Quien tenga interés, le recomiendo el documento Pedagogía de los malabares, de Daniel Sánchez, que os adjuntamos como información extra.
En lugar de seguir ese enfoque, estudiaremos una visión complementaria, usando grafos.
Nota: en un principio no hablamos de cómo empiezan los trucos, asumimos que los trucos ya están en marcha, con todas las pelotas en el aire de modo que en ningún instante futuro esté prevista la caída de dos bolas. Sin embargo, en todos los grafos que dibujaremos hay una forma sencilla de empezar.
Un instante está caracterizado por los tiempos esperados de caída de cada bola. Un estado sólo es válido si cada bola en el aire caerá en un instante futuro distinto. Representamos un estado mediante una secuencia de bola ‘*’ y no bola ‘_’. En la posición i-ésima ponemos una bola si se espera que una bola caiga dentro de i instantes y no-bola si ninguna bola caerá dentro de i instantes. Por ejemplo '**__*' quiere decir que hay tres bolas en el aire y que caerán dentro de 1, 2 y 5 instantes.
Nota: Al estado en el que las bolas caerán en los instantes sucesivos inmediatos, lo denominamos estado fundamental ( '***_' , ó '***__' , ó lo que toque).
La fuerza y la precisión del malabarista limitan el número máximo de instantes en el que futuro al que puede enviar una bola. A este número lo llamamos altura .
Hay una cantidad finita de estados posibles con k bolas y una altura h. Concretamente, cada una de las k bolas caerá en un instante entre 1 y h que es distinto para cada bola, luego se trata de elegir k números entre 1 y h, y la cantidad de formas de hacer esta elección es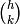 
sage: bolas = 3
sage: altura = 4
sage: estados = [ ''.join(('*' if j in ss else '_') for j in range(altura))
... for ss in Subsets(range(altura), bolas) ]
sage: estados
['***_', '**_*', '*_**', '_***']
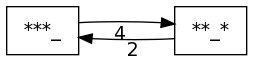
¿A qué estados podemos cambiar partiendo de un estado dado? En el instante siguiente todas las bolas están un instante más próximas a caer en la mano del malabarista, luego pasamos por ejemplo de '_*_**' a '*_**_' , pero si teníamos una bola a punto de caer, el malabarista la recibe y la lanza de forma que caiga dentro de un cierto número de instantes de tiempo, y puede elegir cualquier momento futuro en el que no esté prevista la caída de ninguna otra bola. Por ejemplo, del estado '*_**_' podemos pasar a '**__', '_** * _' o '_**_ * '.
Junto a cada posible transición, guardamos la altura a la que lanzamos la bola (usando un 0 cuando no hacemos nada).
sage: def opciones(estado):
... pasa = estado[1:] + '_'
... if estado[0]=='_': return {pasa:0}
... opciones = {}
... for j,s in enumerate(pasa):
... if s=='_':
... opciones[pasa[:j] + '*'+ pasa[j+1:]] = j + 1
... return opciones
sage: transiciones = dict((estado,opciones(estado)) for estado in estados)
sage: transiciones
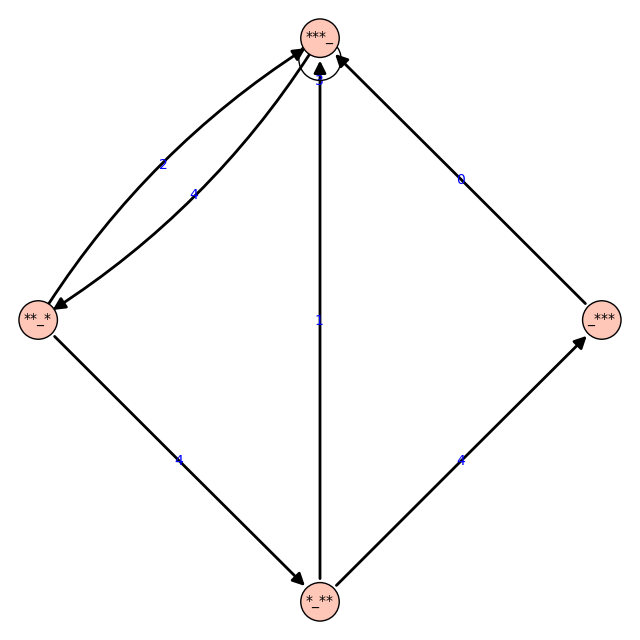
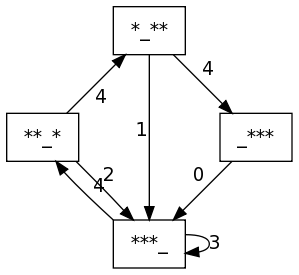
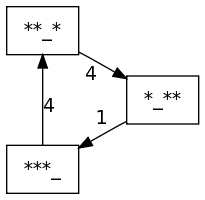
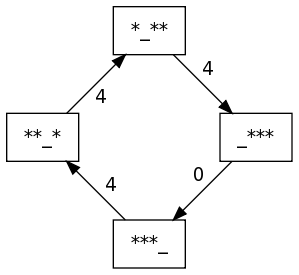
{'***_': {'***_': 3, '**_*': 4}, '_***': {'***_': 0}, '*_**': {'***_': 1, '_***': 4}, '**_*': {'***_': 2, '*_**': 4}}
sage: def grafo_malabar(bolas, altura):
... '''Crea el grafo de malabares con numero de bolas
... y altura dadas'''
... estados = [ ''.join(('*' if j in ss else '_') for j in range(altura))
... for ss in Subsets(range(altura), bolas) ]
...
... transiciones = dict((estado,opciones(estado)) for estado in estados)
... return DiGraph(transiciones)
Dibujamos el grafo
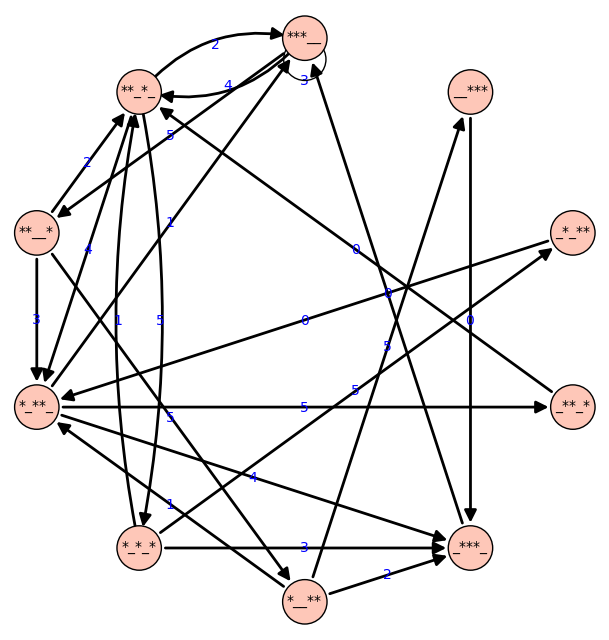
sage: g = grafo_malabar(3,4)
sage: g.show(edge_labels=True, layout='circular', vertex_size=300, figsize=8)
También dibujaremos los diagramas con graphviz, porque las etiquetas se ven más claras (graphviz debe estar instalado).
sage: attach(DATA + 'graphviz.sage')
sage: graphviz(grafo_malabar(3,4))
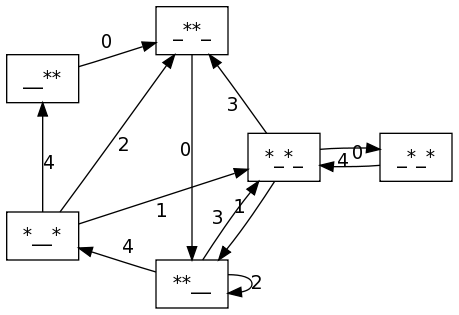
sage: graphviz(grafo_malabar(2,4))
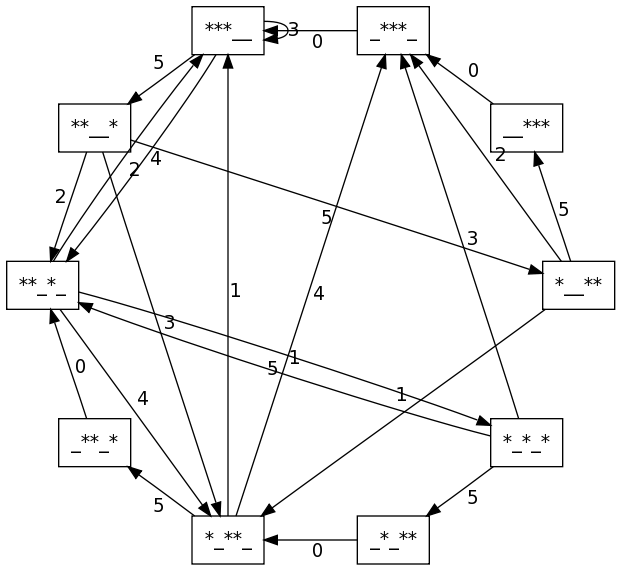
sage: graphviz(grafo_malabar(3,5))
En pocas palabras, los grafos permiten representar situaciones muy diversas de forma muy uniforme.
Requerimientos del espectáculo de lo más variopinto se pueden traducir en restricciones sobre el grafo de posibles malabares.
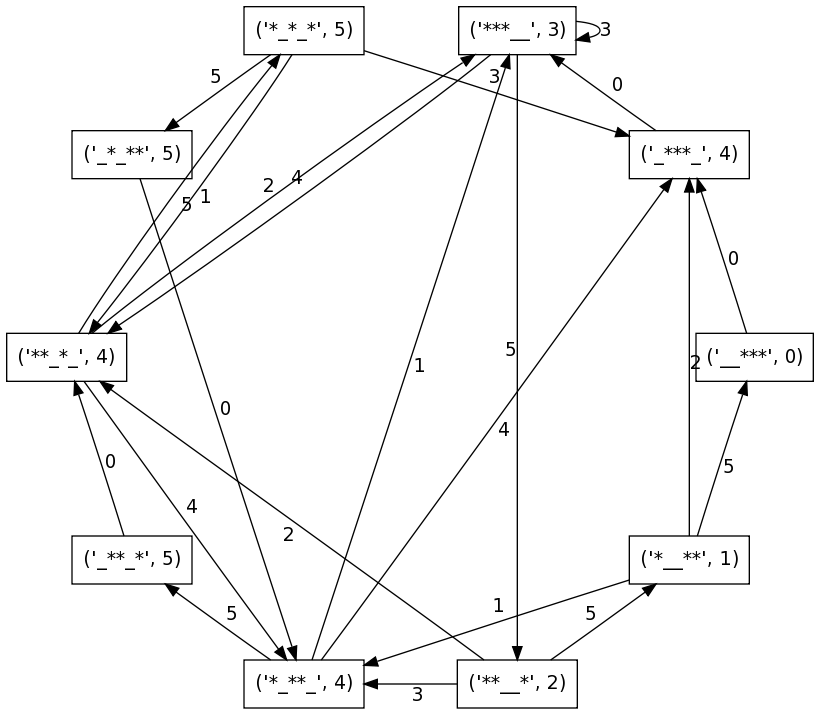
Queremos estar a distancia menor o igual que 4 del estado '___***', por ejemplo porque ese estado nos da tiempo para hacer un truco que hemos preparado, o para saludar a un viandante que ha echado una moneda en el plato.
sage: g = grafo_malabar(3,5)
sage: ds = g.distance_all_pairs()
sage: v0 = '__***'
sage: new_labels = {}
sage: for v in g:
... new_labels[v] = (v, ds[v][v0])
sage: g.relabel(new_labels)
sage: graphviz(g)
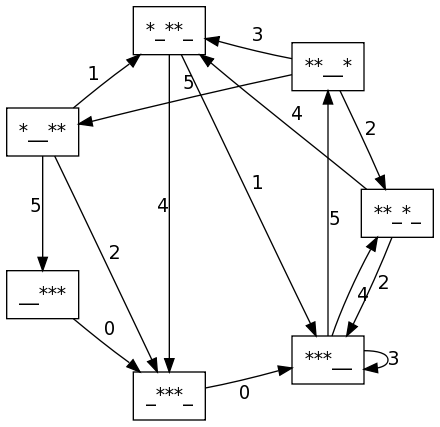
sage: g = grafo_malabar(3,5)
sage: ds = g.distance_all_pairs()
sage: v0 = '__***'
sage: vs0 = [v for v in g if ds[v][v0]<=4]
sage: sg = g.subgraph(vs0)
sage: graphviz(sg)
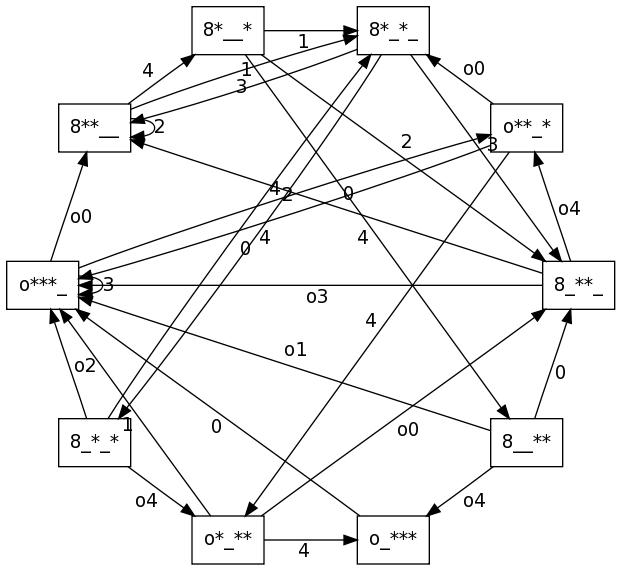
Ahora podemos dejar una pelota en la cabeza por tiempo indefinido. Representamos por un ‘8’ una cabeza con una pelota encima, y por una ‘o’ una cabeza sin pelota encima.
Por ejemplo, para tres pelotas y altura 4, los posibles estados tienen dos pelotas en el aire y una en la cabeza, o tres pelotas en el aire y ninguna en la cabeza.
sage: bolas = 3
sage: altura = 4
sage: estados_con_cabeza = ([('o' + ''.join(('*' if j in ss else '_')
... for j in range(altura)))
... for ss in Subsets(range(altura), bolas) ] +
... [('8' + ''.join(('*' if j in ss else '_')
... for j in range(altura)))
... for ss in Subsets(range(altura), bolas-1) ])
sage: estados_con_cabeza
['o***_', 'o**_*', 'o*_**', 'o_***', '8**__', '8*_*_', '8*__*', '8_**_', '8_*_*', '8__**']
Ahora tenemos opciones nuevas para pasar de un estado a otro:
- Si tenemos la mano vacía y una pelota en la cabeza, podemos cogerla y lanzarla.
- Si tenemos una pelota en la mano y ninguna en la cabeza, podemos dejar la pelota en la cabeza.
- Si tenemos una pelota en la mano y otra en la cabeza, tenemos que lanzar la pelota como de costumbre.
sage: def opciones_con_cabeza(estado):
... cabeza = estado[0]
... mano = estado[1]
... bolas1 = estado[2:] + '_'
... opciones = {}
... if mano=='_' and cabeza=='o':
... opciones = {('o' + bolas1):'0'}
... elif mano=='_': #and cabeza=='8'
... opciones['8' + bolas1] = '0'
... for j,s in enumerate(bolas1):
... if s=='_':
... opciones[('o' + bolas1[:j] +
... '*'+ bolas1[j+1:])] = 'o%d'%(j + 1)
... elif cabeza=='8': #and mano=='*'
... for j,s in enumerate(bolas1):
... if s=='_':
... opciones[('8' + bolas1[:j] +
... '*'+ bolas1[j+1:])] = '%d'%(j + 1)
... else: #cabeza=='o': #and mano=='*'
... opciones['8' + bolas1] = 'o0'
... for j,s in enumerate(bolas1):
... if s=='_':
... opciones[('o' + bolas1[:j] +
... '*'+ bolas1[j+1:])] = '%d'%(j + 1)
... return opciones
sage: def grafo_malabar_con_cabeza(bolas, altura):
... estados_con_cabeza = ([('o' + ''.join(('*' if j in ss else '_')
... for j in range(altura)))
... for ss in Subsets(range(altura), bolas) ] +
... [('8' + ''.join(('*' if j in ss else '_')
... for j in range(altura)))
... for ss in Subsets(range(altura), bolas-1) ])
... transiciones = dict((estado,opciones_con_cabeza(estado))
... for estado in estados_con_cabeza)
... g = DiGraph(transiciones)
... return g
sage: g = grafo_malabar_con_cabeza(3, 4)
sage: graphviz(g)
- Bolas distintas (por su color o por su naturaleza).
- Varios malabaristas.
- ...
Más ejemplos en los ejercicios del final.
Y bien, ¿qué hacemos una vez tenemos un grafo? Para empezar, nos podemos preguntar si el grafo tiene algunas propiedades típicas de la teoría de grafos que pueden ser interesantes:
- ¿El grafo es fuertemente conexo ? Es decir, ¿se puede pasar de un estado a cualquier otro?
- ¿El grafo de malabares es euleriano ? Es decir, ¿existe un circuito que pasa por cada arista exactamente una vez ?
- ¿El grafo de malabares es hamiltoniano ? Es decir, ¿existe un circuito que pasa por cada vértice exactamente una vez ?
sage: for j in range(2,5):
... for k in range(j+1,j+4):
... print 'el grafo malabar con %d bolas y altura %d\
... %ses fuertemente conexo'%(j,k,
... '' if grafo_malabar(j,k).is_strongly_connected() else 'no ')
el grafo malabar con 2 bolas y altura 3 es fuertemente conexo
el grafo malabar con 2 bolas y altura 4 es fuertemente conexo
el grafo malabar con 2 bolas y altura 5 es fuertemente conexo
el grafo malabar con 3 bolas y altura 4 es fuertemente conexo
el grafo malabar con 3 bolas y altura 5 es fuertemente conexo
el grafo malabar con 3 bolas y altura 6 es fuertemente conexo
el grafo malabar con 4 bolas y altura 5 es fuertemente conexo
el grafo malabar con 4 bolas y altura 6 es fuertemente conexo
el grafo malabar con 4 bolas y altura 7 es fuertemente conexo
sage: for j in range(2,5):
... for k in range(j+1,j+4):
... print 'el grafo malabar con %d bolas y altura %d\
... %ses euleriano'%(j,k,
... '' if grafo_malabar(j,k).is_eulerian() else 'no ')
el grafo malabar con 2 bolas y altura 3 no es euleriano
el grafo malabar con 2 bolas y altura 4 no es euleriano
el grafo malabar con 2 bolas y altura 5 no es euleriano
el grafo malabar con 3 bolas y altura 4 no es euleriano
el grafo malabar con 3 bolas y altura 5 no es euleriano
el grafo malabar con 3 bolas y altura 6 no es euleriano
el grafo malabar con 4 bolas y altura 5 no es euleriano
el grafo malabar con 4 bolas y altura 6 no es euleriano
el grafo malabar con 4 bolas y altura 7 no es euleriano
sage: for j in range(2,5):
... for k in range(j+1,j+4):
... print 'el grafo malabar con %d bolas y altura %d\
... %ses hamiltoniano'%(j,k,
... '' if grafo_malabar(j,k).is_hamiltonian() else 'no ')
el grafo malabar con 2 bolas y altura 3 es hamiltoniano
el grafo malabar con 2 bolas y altura 4 no es hamiltoniano
el grafo malabar con 2 bolas y altura 5 no es hamiltoniano
el grafo malabar con 3 bolas y altura 4 es hamiltoniano
el grafo malabar con 3 bolas y altura 5 no es hamiltoniano
el grafo malabar con 3 bolas y altura 6 no es hamiltoniano
el grafo malabar con 4 bolas y altura 5 es hamiltoniano
el grafo malabar con 4 bolas y altura 6 no es hamiltoniano
el grafo malabar con 4 bolas y altura 7 no es hamiltoniano
sage: for j in range(2,5):
... for k in range(j+1,j+4):
... print 'el grafo malabar con %d bolas, altura %d y con cabeza\
... %ses hamiltoniano'%(j,k,
... '' if grafo_malabar_con_cabeza(j,k).is_hamiltonian() else 'no ')
el grafo malabar con 2 bolas, altura 3 y con cabeza es hamiltoniano
el grafo malabar con 2 bolas, altura 4 y con cabeza es hamiltoniano
el grafo malabar con 2 bolas, altura 5 y con cabeza es hamiltoniano
el grafo malabar con 3 bolas, altura 4 y con cabeza es hamiltoniano
el grafo malabar con 3 bolas, altura 5 y con cabeza es hamiltoniano
el grafo malabar con 3 bolas, altura 6 y con cabeza es hamiltoniano
el grafo malabar con 4 bolas, altura 5 y con cabeza es hamiltoniano
el grafo malabar con 4 bolas, altura 6 y con cabeza es hamiltoniano
el grafo malabar con 4 bolas, altura 7 y con cabeza es hamiltoniano
Aunque podemos movernos indefinidamente por el grafo sin seguir necesariamente un patrón periódico, antes o después pasaremos dos veces por el mismo nodo y en ese momento habremos completado un circuito .
Si un circuito pasa dos veces por el mismo sitio, es composición de circuitos elementales o primos, en los que no se pasa dos veces por el mismo vértice.
Los caminos en el grafo son composición de estos caminos elementales. En cierto modo, es equivalente a cómo el desarrollo decimal de un número puede no ser periódico (por ejemplo, el desarollo de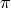 
), pero todos los números se pueden desarrollar con los mismos dígitos.
La teoría de circuitos cerrados en un grafo no dirigido es preciosa y tiene una descripción matemática muy elegante, que en última instancia se debe a se puede definir una suma de caminos. Sin embargo, para grafos dirigidos no se puede definir la suma de caminos y las matemáticas no dan una visión tan clara del conjunto de circuitos. Afortunadamente, existen algoritmos eficientes para encontrar todos los circuitos elementales en un grafo dirigido.
Nota: si listamos la altura a la que debemos lanzar cada pelota (la etiqueta de cada arista), recuperamos la notación siteswap .
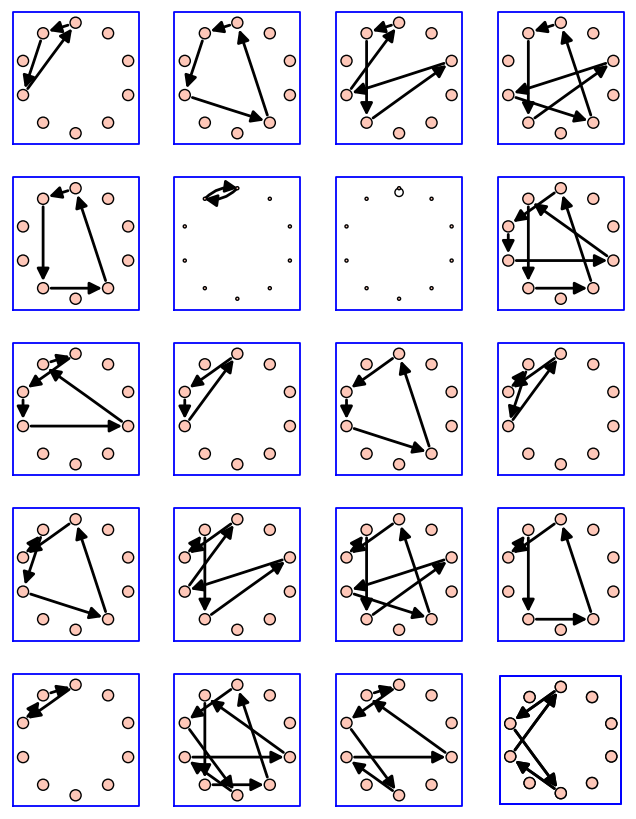
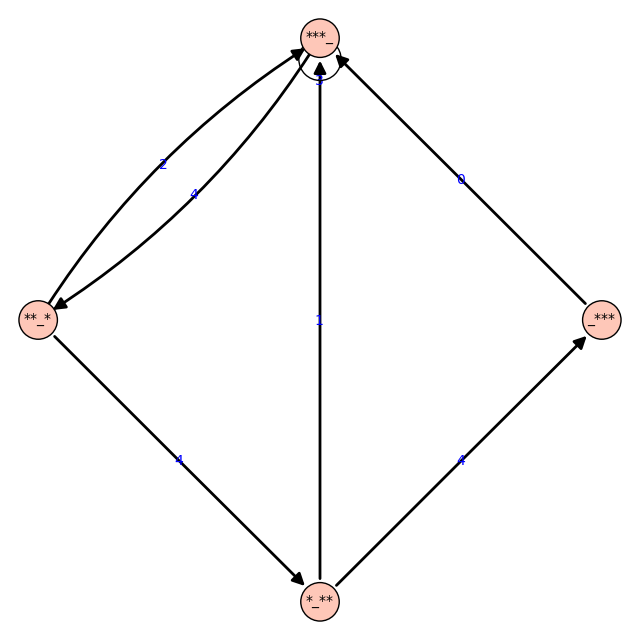
Todos los posibles trucos con 3 bolas y altura a lo sumo 4: listamos los circuitos del grafo malabar con 3 bolas y altura máxima 4, en notación siteswap.
sage: attach(DATA + 'circuits.py')
sage: g = grafo_malabar(3,4)
sage: for ls in circuits(g):
... aristas = [(ls[j],ls[j+1])
... for j in range(len(ls)-1)]
... sg = g.subgraph(edges = aristas)
... print [g.edge_label(v1,v2) for v1,v2 in aristas]
... graphviz(sg)
[3]
[4, 2]
[4, 4, 1]
[4, 4, 4, 0]
sage: g = grafo_malabar(3,4)
sage: g.show(edge_labels=True, layout='circular', vertex_size=300, figsize=8)
sage: graphs_list.show_graphs([g.subgraph(edges = [(ls[j],ls[j+1])
... for j in range(len(ls)-1)])
... for ls in circuits(g)])
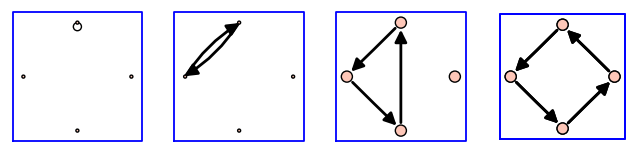
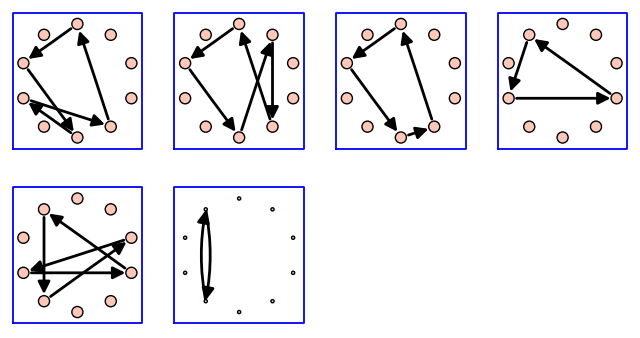
Todos los posibles trucos con 3 bolas y altura a lo sumo 5.
sage: attach(DATA + 'circuits.py')
sage: g = grafo_malabar(3,5)
sage: for ls in circuits(g):
... aristas = [(ls[j],ls[j+1])
... for j in range(len(ls)-1)]
... print ''.join([str(g.edge_label(v1,v2)) for v1,v2 in aristas])
441
4440
45501
455040
4530
42
3
5350530
53502
531
5340
5241
52440
525501
5255040
52530
522
55150530
551502
5511
55140
55500
5520
450
55050
51
La misma información, de forma gráfica.
sage: g = grafo_malabar(3,5)
sage: show(g, edge_labels=True, layout='circular', figsize = 8, vertex_size=400)
sage: graphs_list.show_graphs([g.subgraph(edges = [(ls[j],ls[j+1])
... for j in range(len(ls)-1)])
... for ls in circuits(g)])
