Please write a title for this worksheet!
TODO: merge con el ejercicio del caballo que está en canijo
- Encuentra el recorrido de longitud más corta que pasa una vez por cada arista, para el problema de recogida de basuras.
- Escribe el grafo de malabares con dos pelotas de un color y una tercera de otro color y altura máxima 4. Si la tercera pelota es una manzana, identifica los estados en los que puedes pegarle un mordisco.
- Pepito está aprendiendo a hacer malabares con cuchillos. Se ve capaz de lanzar y recibir los cuchillos a altura 5 pero no quiere lanzar dos cuchillos seguidos tan alto por si se hace un lío al recogerlos. Modifica el grafo de tres objetos y altura 5 para evitar lanzar dos objetos a altura 5 seguidos.
- Al hablar de páginas web mencionamos un motivo por el que una cadena de Markov podría converger a una u otra distribución de probabilidad dependiendo del punto de partida. Muestra un grafo concreto que tenga este problema.
- Estudia el problema de la convergencia en el circuito con dos vértices, que te mostramos abajo: ¿converge la distribución de probabilidad de los caminos aleatorios que comienzan en el vértice 0? ¿y en el vértice 1? ¿se aplica tu razonamiento a todos los circuitos de cualquier longitud?
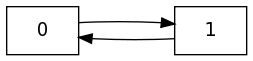
- Encuentra otro grafo fuertemente conexo, y que no sea un circuito, pero tal que la distribución de probabilidad no converja desde algún punto de partida.
- Busca en la literatura (o en internet, pero llegando a una fuente de confianza), las hipótesis bajo las cuales la distribución de probabilidad de una cadena de Markov converge a una misma distribución de probabilidad, independientemente del punto de partida. Razona si los grafos que vimos al estudiar el problema de evolución verifican esta propiedad.
