- Simula el siguiente experimento: lanza monedas cargadas que dan cara con probabilidad p y cruz con probabilidad 1-p hasta obtener la primera cara, y anota el número de cruces que has obtenido. Dibuja un histograma de 1000 extracciones aleatorias siguiendo este esquema, para un valor de p que tú elijas.
- Compara el resultado con el histograma de 1000 extracciones de una distribución geométrica con probabilidad p.
El cuantil de orden p o p-cuantil, para 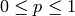 , de una distribución de probabilidad es el valor
, de una distribución de probabilidad es el valor 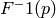 , donde F es la función de distribución. La función cuantil es la función Q(p) que a cada p le asocia su p-cuantil. En principio, esta definición se aplica a distribuciones continuas, pero se puede extender a distribuciones de probabilidad finitas y discretas, si tomamos:
, donde F es la función de distribución. La función cuantil es la función Q(p) que a cada p le asocia su p-cuantil. En principio, esta definición se aplica a distribuciones continuas, pero se puede extender a distribuciones de probabilidad finitas y discretas, si tomamos:
Escribe funciones que devuelvan el p-cuantil de una distribución de probabilidad (en versiones finita, discreta y continua). Razona sobre la relación entre estas funciones y las extracciones aleatorias que vimos en teoría.
Una forma gráfica bastante común de visualizar si dos distribuciones de probabilidad son similares es el QQ-plot . La letra Q se refiere a los cuantiles (” quantiles ” en inglés). Si tenemos dos distribuciones f y g:
- Tomamos un entero k y calculamos la lista de los k-1 cuantiles de orden 1/k, 2/k, ... (k-1)/k, de f (sean
) y la lista correspondiente con los cuantiles de g (sean
).
- Dibujamos para cada j entre 1 y k-1 todos los puntos
.
- Si las distribuciones son iguales, los puntos dibujados están todos en la diagonal. Si son la misma distribución, pero desplazadas una distancia d (por ejemplo, si las funciones de densidad satisfacen g(x)=f(x-d)), los puntos estarán en la recta y=x+d.
Dibuja qqplots que comparen los siguientes pares de distribuciones:
- Una binomial con n lanzamientos y p=1/2 con una normal de media np y varianza np(1-p), para varios valores de n.
- Una poisson de parámetro
con una normal de media
y varianza
, para un valor pequeño de
y otro mayor.
¿Cómo podemos estimar la distancia entre dos distribuciones de probabilidad? Queremos que por ejemplo la distancia entre la distribución que toma el valor x con probabilidad 1 y la que toma el valor y con probabilidad 1 sea |x-y|, y que la distancia entre una distribución y ella misma sea 0. Ésto último descarta por ejemplo tomar el valor esperado de la distancia entre las dos variables aleatorias.
La idea del qqplot se puede llevar un poco más lejos: tomar como distancia entre las distribuciones el promedio de las distancias entre los cuantiles del mismo orden. Para mayor número de cuantiles, tenemos una medida más fina.
Estudia si esta medida verifica las condiciones de arriba y si merece que la llamemos una distancia.
Definimos dos variables aleatorias X e Y de la forma siguiente:
- El espacio muestral son las permutaciones de los números del 1 al 10.
- La medida es la medida uniforme, que a cada permutación le da probabilidad 1/10!.
- X(w) es la imagen de 1 por la permutación w. Y(w) es la imagen de 2 por la permutación w.
Se te pide lo siguiente:
- Almacena en un diccionario la distribución conjunta de X y de Y: los pares son tuplas (x,y), y el valor asociado al par (x,y) es la probabilidad de que X valga x e Y valga y.
- Calcula la distribución marginal de X y la de Y. Confirma que obtienes el resultado esperado.
- Calcula la covarianza de X y de Y.
- Calcula la distribucion de X condicionada a que Y es multiplo de 3.