En esta sesión vamos a enumerar varias familias de objetos combinatorios, igual que hicimos en la primera sesión, pero ahora además de enumerar objetos los contaremos sin enumerarlos, para hacer más patente la relación entre una construcción recursiva y las fórmulas recursivas para el número de elementos que son habituales en combinatoria. El primer ejemplo está resuelto, los dos siguientes son ejercicios que resolveremos en clase, y los dos últimos son una práctica a entregar.
Estudiamos las formas de descomponer un número n como suma de exactamente k enteros positivos. Listamos los números de cada partición de mayor a menor, para evitar repeticiones. Observamos que las particiones pertenecen a dos clases:
- Las que terminan en 1.
- Las que tienen todos sus elementos mayores o iguales a 2.
Esta idea nos permite construir las particiones recursivamente:
- Generamos las particiones de n-1 en k-1 partes iguales, y añadimos un 1 al final para dar cuenta del primer grupo de particiones.
- Generamos las particiones de n-k en k partes iguales, y sumamos 1 a cada elemento para dar cuenta del segundo grupo de particiones.
sage: def particiones_k(total, partes):
... if partes == total:
... return [[1]*total]
... if partes == 1:
... return [[total]]
... if not(0 < partes < total):
... return []
... ls1 = [p+[1] for p in particiones_k(total-1, partes-1)]
... ls2 = [[parte+1 for parte in p] for p in particiones_k(total-partes, partes)]
... return ls1 + ls2
sage: particiones_k(8,3)
[[6, 1, 1], [5, 2, 1], [4, 3, 1], [4, 2, 2], [3, 3, 2]]
sage: #Las particiones sin restricciones (que vimos en la sesion 1)
sage: #se pueden obtener facilmente a partir de particiones_k
sage: def particiones(total):
... return [ls for j in range(1,total+1)
... for ls in particiones_k(total, j)]
sage: particiones(5)
[[5], [4, 1], [3, 2], [3, 1, 1], [2, 2, 1], [2, 1, 1, 1], [1, 1, 1, 1, 1]]
Si sólo queremos contar el número de particiones de n con k elementos (en adelante 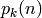 ), las reglas de recursión anteriores se traducen en la siguiente ecuación de recurrencia:
), las reglas de recursión anteriores se traducen en la siguiente ecuación de recurrencia:
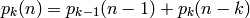
junto con los “datos de frontera”:
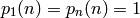
y:
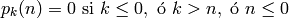
sage: def n_particiones_k(total, partes):
... if partes == total:
... return 1
... if partes == 1:
... return 1
... if not(0 < partes < total):
... return 0
... n1 = n_particiones_k(total-1, partes-1)
... n2 = n_particiones_k(total-partes, partes)
... return n1 + n2
sage: n_particiones_k(8,3)
5
Obviamente, se tarda menos tiempo en contar las posibilidades que en construirlas todas explícitamente.
sage: time n_particiones_k(60,10)
62740
Time: CPU 0.10 s, Wall: 0.10 s
sage: time ls = particiones_k(60,10)
Time: CPU 2.19 s, Wall: 2.20 s
En el ejemplo anterior hemos transportado la definición recursiva directamente a nuestro código, pero vimos en el bloque II que este enfoque nos puede traer problemas, al usar una definición recursiva para calcular los números de fibonacci:
def fibo(n):
if n<2:
return 1
return fibo(n-1) + fibo(n-2)
En este ejemplo paradigmático, estimamos que para calcular el número de fibonacci n-ésimo se hacían aproximadamente tantas llamadas recursivas a fibo como el número de fibonacci n-ésimo (más exactamente, el número I(n) de llamadas a fibo para calcular fibo(n) es: I(n-1)+I(n-2)+1). Usando la técnica del ” profiler ” de la sesión b3s3, medimos exactamente el número de llamadas para confirmar este hecho:
sage: def fibo(n):
... if n<2:
... return 1
... return fibo(n-1) + fibo(n-2)
Observamos la columna ncalls que indica el número de llamadas a una función. Comprueba para unos pocos valores que se satisface la fórmula de recurrencia mencionada.
sage: #importamos los modulos cProfile y pstats para ver las estadisticas
sage: #de cuanto tiempo se pasa en cada parte del codigo
sage: import cProfile, pstats
sage: #No necesitamos entender la siguiente linea:
sage: #tomalo como una version avanzada de timeit
sage: cProfile.runctx("fibo(10)", globals(), locals(), DATA + "Profile.prof")
sage: s = pstats.Stats(DATA + "Profile.prof")
sage: #Imprimimos las estadisticas, ordenadas por el tiempo total
sage: s.strip_dirs().sort_stats("time").print_stats()
Mon Feb 21 22:57:30 2011 /home/sageadm/nbfiles.sagenb/home/pang/295/data/Profile.prof
179 function calls (3 primitive calls) in 0.000 CPU seconds
Ordered by: internal time
ncalls tottime percall cumtime percall filename:lineno(function)
177/1 0.000 0.000 0.000 0.000 ___code___.py:3(fibo)
1 0.000 0.000 0.000 0.000 <string>:1(<module>)
1 0.000 0.000 0.000 0.000 {method 'disable' of '_lsprof.Profiler' objects}
<pstats.Stats instance at 0x9a68d40>
En nuestro ejemplo anterior, ocurre algo similar, porque al llamar a particiones_k(n,k) llamamos recursivamente a particiones_k(n-k,k) y a particiones_k(n-1,k-1) , lo que eventualmente implica que llamaremos varias veces a particiones_k(n,k) con los mismos argumentos.
A modo de confirmación, el sentido común nos dice que para calcular n_particiones_k(n,k) , necesitaremos como mucho n*k llamadas recursivas a n_particiones_k , lo que corresponde a llamar a la función con todos los posibles valores menores que n y con los menores que k. Sin embargo, el número de llamadas a n_particiones_k(40,10) es 9111, mucho mayor que 400.
sage: #importamos los modulos cProfile y pstats para ver las estadisticas
sage: #de cuanto tiempo se pasa en cada parte del codigo
sage: import cProfile, pstats
sage: #No necesitamos entender la siguiente linea:
sage: #tomalo como una version avanzada de timeit
sage: cProfile.runctx("n_particiones_k(40,10)", globals(), locals(), DATA + "Profile.prof")
sage: s = pstats.Stats(DATA + "Profile.prof")
sage: #Imprimimos las estadisticas, ordenadas por el tiempo total
sage: s.strip_dirs().sort_stats("time").print_stats()
Mon Feb 21 22:57:30 2011 /home/sageadm/nbfiles.sagenb/home/pang/295/data/Profile.prof
9113 function calls (3 primitive calls) in 0.014 CPU seconds
Ordered by: internal time
ncalls tottime percall cumtime percall filename:lineno(function)
9111/1 0.014 0.000 0.014 0.014 ___code___.py:3(n_particiones_k)
1 0.000 0.000 0.014 0.014 <string>:1(<module>)
1 0.000 0.000 0.000 0.000 {method 'disable' of '_lsprof.Profiler' objects}
<pstats.Stats instance at 0x9a68ef0>
En otros lenguajes como Haskell , las definiciones anteriores no provocan esta cascada de llamadas recursivas . Esto se debe a que Haskell es un lenguaje funcional puro, lo que implica entre otras cosas que todas las llamadas a una función con los mismos argumentos producen siempre el mismo resultado. Gracias a este conocimiento, el compilador no necesita ejecutar una función la segunda vez que la llaman con unos argumentos dados, porque ya ha calculado el valor una vez.
En python, ésto no es necesariamente cierto (piensa por ejemplo en las funciones que generan números aleatorios), pero podemos crear una función que guarde los valores de las llamadas en memoria, usando el decorador @cached_function , que altera una función para que almacene los valores de cada llamada, y así evitar calcular dos veces el valor de la función con los mismos argumentos.
sage: @cached_function
sage: def n_particiones_k_cached(total, partes):
... if partes == total:
... return 1
... if partes == 1:
... return 1
... if not(0 < partes < total):
... return 0
... n1 = n_particiones_k_cached(total-1, partes-1)
... n2 = n_particiones_k_cached(total-partes, partes)
... return n1 + n2
Verificamos que el número de llamadas recursivas desciende drásticamente (en este caso, a 248).
sage: #importamos los modulos cProfile y pstats para ver las estadisticas
sage: #de cuanto tiempo se pasa en cada parte del codigo
sage: import cProfile, pstats
sage: #No necesitamos entender la siguiente linea:
sage: #tomalo como una version avanzada de timeit
sage: cProfile.runctx("n_particiones_k_cached(40,10)", globals(), locals(), DATA + "Profile.prof")
sage: s = pstats.Stats(DATA + "Profile.prof")
sage: #Imprimimos las estadisticas, ordenadas por el tiempo total
sage: s.strip_dirs().sort_stats("time").print_stats()
Mon Feb 21 22:57:31 2011 /home/sageadm/nbfiles.sagenb/home/pang/295/data/Profile.prof
4630 function calls (4019 primitive calls) in 0.017 CPU seconds
Ordered by: internal time
ncalls tottime percall cumtime percall filename:lineno(function)
365 0.011 0.000 0.013 0.000 function_mangling.py:205(fix_to_pos)
365/1 0.002 0.000 0.017 0.017 cachefunc.py:96(__call__)
248/1 0.001 0.000 0.017 0.017 ___code___.py:3(n_particiones_k_cached)
365 0.001 0.000 0.013 0.000 cachefunc.py:188(get_key)
365 0.000 0.000 0.000 0.000 {range}
365 0.000 0.000 0.000 0.000 {method 'has_key' of 'dict' objects}
365 0.000 0.000 0.000 0.000 {sorted}
730 0.000 0.000 0.000 0.000 {method 'append' of 'list' objects}
365 0.000 0.000 0.000 0.000 function_mangling.py:261(<genexpr>)
365 0.000 0.000 0.000 0.000 cachefunc.py:119(get_cache)
365 0.000 0.000 0.000 0.000 {len}
365 0.000 0.000 0.000 0.000 {method 'keys' of 'dict' objects}
1 0.000 0.000 0.017 0.017 <string>:1(<module>)
1 0.000 0.000 0.000 0.000 {method 'disable' of '_lsprof.Profiler' objects}
<pstats.Stats instance at 0x9a7ccb0>
Cuestión : Vuelve a ejecutar el código de arriba, sin modificarlo. Explica el resultado. Usa la acción “Restart Worksheet”, y ejecútalo de nuevo (ejecuta antes el cuadro que define n_particiones_k_cached ). Explica el resultado.
Estudiamos las palabras formadas por 0 y 1 tales que no hay dos unos consecutivos. Hay dos palabras de longitud 1 con esta propiedad:‘0’ y ‘1’, tres de longitud 2: ‘00’, ‘01’, ‘10’, 5 de longitud 3: ‘000’, ‘001’, ‘010’, ‘100’, ‘101’. Las palabras se pueden generar de forma recursiva siguiendo la regla siguiente:
- Las palabras que terminan en ‘0’ se pueden extender con un ‘0’ o con un ‘1’
- Las palabras que terminan en ‘1’ sólo se pueden extender con un ‘0’.
También puedes seguir la siguiente regla equivalente para generar todas las palabras de longitud k:
- Añade un ‘0’ a todas las palabras de longitud k-1.
- Añade un ‘01’ a todas las palabras de longitud k-2.
Ejercicio
- Escribe código que genere todas las palabras de este tipo hasta longitud k.
- Escribe (y justifica) una ecuación de recursión para el número total de palabras de este tipo: ¿te resulta familiar?
- Construye los caminos colocando las palabras en un árbol y usando SearchForest. Los hijos de una palabra que termina en ‘0’ son la misma palabra seguida de ‘0’ y de ‘1’, mientras que el único hijo de una palabra que termina en ‘1’ es la misma palabra seguida de ‘0’. En este caso el bosque tiene dos nodos raíces, el ‘0’ y el ‘1’.
El triángulo de Pascal registra el número de caminos desde el vértice superior hasta un vértice cualquiera, tales que en cada paso descendemos de una fila a la inmediatamente inferior mediante una de las aristas descendientes: bien a la izquierda bien a la derecha.
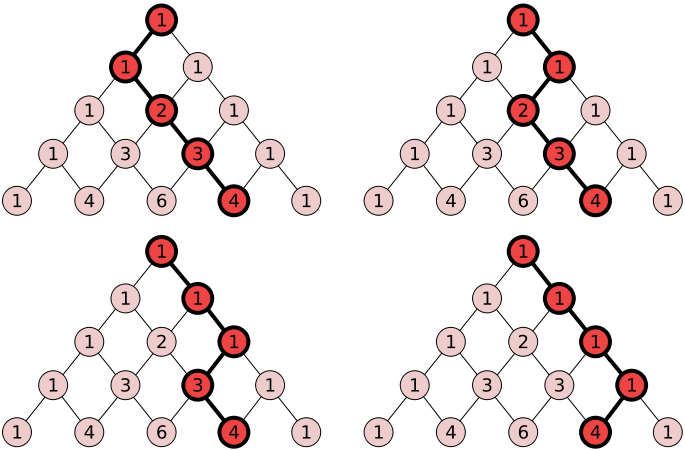
Codificamos los caminos como secuencias con las letras I y D. Por ejemplo el camino que está arriba a la izquierda del diagrama corresponde a la secuencia ‘IDDD’, mientras que el camino de abajo a la derecha corresponde a ‘DDDI’.
La siguiente recursión permite encontrar todos los caminos que llevan del vértice superior al vértice en la fila n y la columna k:
- Encuentra todos los caminos que llevan a la posición (n-1, k-1) y añádeles una ‘D’.
- Encuentra todos los caminos que llevan a la posición (n-1, k) y añádeles una ‘I’.
Ejercicio :
- Aplica la recursión anterior para calcular todos los caminos que llevan del vértice superior al vértice en la fila n y la columna k. Deberías obtener exactamente
tales caminos.
- Escribe (y justifica) una ecuación de recursión para el número total de caminos basada en la recursión anterior: ¿te resulta familiar?
- Construye los caminos colocando los caminos parciales en un árbol y usando SearchForest. Los caminos parciales son caminos desde el vértice superior hasta otro vértice que son susceptibles de ser continuados hasta el vértice (n,k) siguiendo las reglas del juego.
Los dos ejercicios que siguen constituyen la entrega del bloque IV, que por supuesto es opcional. Vale un total de 7 puntos.
Hay dos formas de agrupar tres letras (por ejemplo, para realizar una operación matemática asociativa sobre varios símbolos, pero sin alterar el orden de las letras)
(a(bc)), ((ab)c)
Hay cinco formas de agrupar cuatro letras:
(a((bc)d)), (a(b(cd))), ((ab)(cd)), (((ab)c)d), ((a(bc))d)
La siguiente recursión permite encontrar todas las formas. Partimos de una secuencia de letras, ‘abcd’:
- Partimos la secuencia en todos los posibles puntos: [‘a’, ‘bcd’], [‘ab’, ‘cd’], [‘abc’,’d’]
- Agrupamos cada parte recursivamente de todas las formas posibles. Por ejemplo, ‘bcd’ se puede agrupar como ‘(b(cd))’ y como ‘((bc)d)’
- Unimos cada forma de agrupar las letras de la izquierda con cada forma de agrupar las letras de la derecha, y encerramos el resultado entre paréntesis. Ej, ‘a’, ‘((bc)d)’ -> ‘(a((bc)d))’ (las letras sueltas no necesitan paréntesis)
Ejercicio
- Aplica la recursión anterior para construir todas las formas de agrupar n letras.
- Escribe (y justifica) una ecuación de recursión para el número total de posibilidades. Cuenta el número de posibilidades G(n) para n desde 1 hasta 10.
Consideramos ahora los caminos monótonos , en la forma siguiente: todos los caminos que unen el vértice (0,0) con el vértice (n,n) avanzando hacia la derecha (‘D’) y hacia arriba (‘A’), tales que en todo momento hemos avanzado al menos tantos pasos hacia la derecha como hemos avanzado hacia arriba.
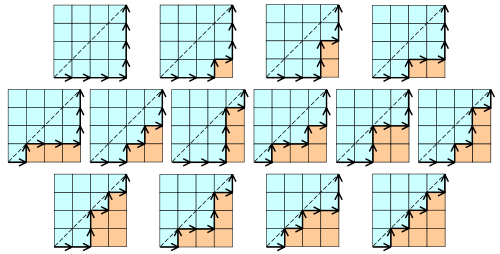
Sea C(n) el número total de caminos que llegan al vértice (n,n) partiendo del vértice (0,0). Llamaremos a estos caminos “diagonales” porque terminan en la misma diagonal en la que empiezan.
¿Cómo podemos encontrar una fórmula de recursión para C(n)? Observamos que todos los caminos siguen la siguiente estructura: comienzan con un movimiento a la derecha, luego sigue un camino diagonal (posiblemente vacío), luego viene un movimiento hacia arriba que compensa el primer movimiento a la derecha, y luego viene otro camino diagonal (posiblemente vacío). En el siguiente diagrama, los puntos rojo y verde marcan el principio y el fin del primer camino diagonal.
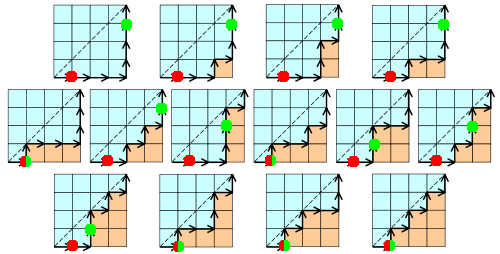
Ejercicio
- Aplica la recursión anterior para construir todos los caminos . Codifica los caminos como secuencias con las letras D y A, que indican en qué momentos debemos movernos a la derecha o hacia arriba. Por ejemplo, el diagrama de abajo a la derecha corresponde al camino ‘DADADADA’, y el de arriba a la izquierda al camino ‘DDDDAAAA’ .
- Escribe (y justifica) una ecuación de recursión para el número total de caminos de este tipo. Calcula C(n) para n desde 1 hasta 10.
- Sustituye la letra ‘D’ por el carácter ‘(‘ y la letra ‘A’ por el carácter ‘)’. Describe el resultado.
Los ejemplos están extraídos del capítulo 6 del libro de texto de la asignatura de matemática discreta, que puedes consultar como referencia:
http://www.uam.es/personal_pdi/ciencias/gallardo/cap6-MD-2010-2011.pdf
del libro de Sage en francés:
http://sagebook.gforge.inria.fr/
y de la wikipedia:
Los dos ejercicios que siguen constituyen la entrega del bloque IV, que por supuesto es opcional. Vale un total de 7 puntos.