En la primera sesión de este bloque aprendimos a recorrer exhaustivamente un conjunto de posibilidades para contar las que satisfacían una propiedad, y así calcular probabilidades como el número de casos favorables dividido por el número de casos posibles. En algunos casos el número de posibilidades es enorme, y el resultado, realmente mucho más preciso de lo que necesitábamos.
Una alternativa consiste en calcular sólo unos cuantos casos extraídos aleatoriamente, y hacer una estadística de los casos favorables entre los posibles. A esta estrategia se le llama en general el método de Monte Carlo, por su uso del azar. Aunque el resultado sólo es aproximado, es fácil controlar el tiempo de cómputo que destinamos a aproximar la solución.
Por supuesto, en muchos casos es posible hacer el cálculo exacto mediante razonamiento puro y, aún en los casos en que no es así, el razonamiento puede servir para reducir el número de posibilidades a explorar, o hacer más eficiente un método de Monte Carlo.
Como ejemplo, nos planteamos este problema: partiendo de una masa para hacer galletas que contiene un total de P pasas, hacemos G galletas. Asumiendo que cada pasa terminará en una de las G galletas con la misma probabilidad y de forma independiente a la galleta de destino de las otras pasas, calcula la probabilidad de que cada galleta tenga al menos k pasas.
Para distribuir las pasas de todas las formas posibles, contamos cada posible lista de P valores
![[G_1,G_2,\dots,G_P]](_images/math/99032df50f2ca9dc6e0bf85d3bfb495807314c8c.png)
donde el primer valor indica la galleta en que termina la primera pasa, y así sucesivamente. Como cada pasa puede terminar en una de las G galletas posibles, el número total de posibilidades es 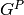 .
.
sage: def pasas(G,P,k):
... '''Calcula cuantas formas de repartir P pasas entre G galletas
... dejan al menos k pasas en cada galleta
... '''
... favorables = 0
... #Cada pasa termina en una galleta distinta, total G^P posibilidades
... for j in srange(G^P):
... #lista que indica en que galleta esta cada pasa
... donde_esta_la_pasa = j.digits(base=G,padto=P)
... #G galletas, que comienzan sin pasas
... pasas_en_cada_galleta = [0]*G
... #Contamos el numero de pasas en cada galleta
... for g in donde_esta_la_pasa:
... pasas_en_cada_galleta[g] += 1
... if min(pasas_en_cada_galleta)>=k:
... favorables += 1
... return favorables/G^P
sage: %time
sage: pasas(4,6,1)
195/512
CPU time: 0.17 s, Wall time: 0.19 s
sage: %time
sage: pasas(3,7,1)
602/729
CPU time: 0.09 s, Wall time: 0.10 s
sage: %time
sage: pasas(4,7,1)
525/1024
CPU time: 0.66 s, Wall time: 0.67 s
Como vemos, este enfoque requiere mucho tiempo incluso para cantidades pequeñas de pasas y de galletas. No en vano hay que iterar el bucle principal ¡¡G^P veces!!. Como el problema no tiene mucha gracia si el número de pasas no es al menos igual al número de galletas, estamos hablando de crecimiento exponencial. Aunque se pueden usar varios trucos para reducir el tiempo de cómputo, sigue siendo un crecimiento muy rápido.
Usando el método de Monte Carlo, decidimos exactamente el número de veces que iteramos el bucle.
Nota: este problema se puede resolver de forma exacta, pero no es trivial.
Nota: la lista de galletas de cada pasa contiene información redundante para este problema, en el que sólo nos interesa el total de pasas en cada galleta. Por ejemplo, podemos usar IntegerVectors para recorrer las listas de enteros de longitud G que suman P (el número de pasas en cada galleta), pero distintas formas de recorrer el conjunto pueden responder a distintos modelos de probabilidad.
sage: def pasas_mc(G,P,k,T):
... '''Calcula cuantas formas de repartir P pasas entre G galletas
... dejan al menos k pasas en cada galleta, usando un método de
... Monte Carlo con muestra de tamaño T
... '''
... favorables = 0
... for h in xrange(T):
... #lista que indica en que galleta esta cada pasa
... #Usamos randint que devuelve un entero escogido
... #aleatoriamente en un rango
... donde_esta_la_pasa = [randint(0,G-1) for j in range(P)]
... #G galletas, que comienzan sin pasas
... pasas_en_cada_galleta = [0]*G
... #Contamos el numero de pasas en cada galleta
... for g in donde_esta_la_pasa:
... pasas_en_cada_galleta[g] += 1
... if min(pasas_en_cada_galleta)>=k:
... favorables += 1
... return favorables/T
sage: #Distintas llamadas a esta funcion con los mismos argumentos
sage: #no devuelven el mismo resultado, debido al uso de numeros
sage: #aleatorios
sage: #Cuanto mayor la muestra, menor la oscilacion
sage: p = pasas_mc(4,7,1,1000)
sage: print p, p.n()
63/125 0.504000000000000
El método de Monte Carlo permite abordar problemas que no se pueden resolver por fuerza bruta contando todas las posibilidades.
En el siguiente ejemplo sencillo, lanzamos monedas al aire (monedas equilibradas, lanzamientos independientes) hasta que acumulamos un cierto número de caras, ¿cuántos lanzamientos necesitamos en promedio para obtener al menos k caras?
Podemos simular este experimento usando llamadas a randint(0,1) para simular lanzamientos de monedas. Si el número devuelto es 0, lo tomamos como una cruz, si es un 1, como una cara. Repetimos el experimento hasta que acumulemos k caras, y tomamos nota del número de lanzamientos que hemos necesitado.
sage: def geometrica_mc(k,T):
... '''Número medio de lanzamientos hasta obtener k caras, por
... el método de Monte Carlo
... '''
... lanzamientos = 0
... for j in range(T):
... caras = 0
... while caras<k:
... lanzamientos += 1
... caras += randint(0,1)
...
... promedio = lanzamientos/T
... return promedio
sage: m = geometrica_mc(4,10000)
sage: print m, m.n()
79953/10000 7.99530000000000
En este caso, obtenemos la confirmación no de la fuerza bruta, sino del razonamiento, porque el número esperado de lanzamientos es claramente 2k (hecho que sabréis demostrar cuando estudiéis la binomial negativa en probabilidad).
¿Cuántas matrices cuadradas cuyas entradas sean 0 ó 1 son invertibles en 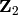 ? Podemos dar a este enunciado una interpretación probabilista: ¿cuál es la probabilidad de que una matriz KxK en
? Podemos dar a este enunciado una interpretación probabilista: ¿cuál es la probabilidad de que una matriz KxK en 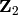 cuyas entradas han sido escogidas de forma aleatoria e independiente entre 0 y 1 sea invertible?
cuyas entradas han sido escogidas de forma aleatoria e independiente entre 0 y 1 sea invertible?
Es fácil generar una matriz cuadrada cuyas entradas son enteros escogidos aleatoriamente entre 0 y 1. Para calcular su determinante en 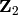 , calculamos su determinante habitual y tomamos el resto de dividir por 2. Alternativamente, podríamos usar el cuerpo Integers(2) y su método random_element() .
, calculamos su determinante habitual y tomamos el resto de dividir por 2. Alternativamente, podríamos usar el cuerpo Integers(2) y su método random_element() .
Recordamos una forma cómoda de construir matrices en Sage:
M = matrix(ZZ, K1, K2, lista)
donde K1 es el número de filas y K2 el número de columnas y, en vez de pasar una lista con las filas, pasamos una sóla lista con K1xK2 elementos.
También podemos usar random_matrix , pero es un método menos general.
sage: K=6
sage: #Generar una matriz con entradas 0 o 1 escogidas de forma aleatoria
sage: lista = [randint(0,1) for j in range(K*K)]
sage: M = matrix(ZZ,K,K, lista)
sage: print M, det(M)%2
[0 0 1 0 0 1]
[0 0 1 0 1 1]
[1 1 1 1 1 0]
[1 0 1 0 0 1]
[1 0 1 0 1 1]
[0 1 0 1 1 0] 0
Calcula la probabilidad por fuerza bruta contando los casos favorables y por el método de Monte Carlo.
¿Y si cambiamos la probabilidad, y hacemos el 1 más probable que el 0? ¿Conseguiremos con ello aumentar la probabilidad de obtener matrices invertibles?
Para plantearnos este problema necesitamos extraer un 0 ó un 1 con una probabilidad ![p\in [0,1]](_images/math/6af8dedac53be4afc06c4365383b58df525aa46b.png) . La manera estándar de hacer ésto es usar la función random(), que devuelve un número aleatorio entre 0 y 1. Si el número extraido es menor que p, anotamos un 1 y si es mayor, anotamos un 0.
. La manera estándar de hacer ésto es usar la función random(), que devuelve un número aleatorio entre 0 y 1. Si el número extraido es menor que p, anotamos un 1 y si es mayor, anotamos un 0.
sage: K = 6
sage: p = 0.7
sage: #Construimos una matriz KxK de ceros:
sage: M = matrix(ZZ,K,K)
sage: #Rellenamos las entradas de la matriz con 0 o 1:
sage: for j in range(K):
... for k in range(K):
... t = random()
... if t<p:
... M[j,k]=1
sage: print M
[1 1 1 1 1 1]
[1 1 1 0 1 1]
[1 0 1 1 1 0]
[1 1 1 1 1 1]
[1 1 0 1 1 0]
[1 0 1 1 0 1]
sage: #codigo alternativo
sage: def aleatoriop(p):
... if random()<t:
... return 1
... return 0
sage: p = 0.7
sage: lista = [aleatoriop(p) for j in range(K*K)]
sage: M = matrix(ZZ,K,K, lista)
Traceback (most recent call last):
...
SyntaxError: invalid syntax
En esta sesión hemos usado los generadores de números aleatorios del ordenador, llamando a las funcioens randint y random . Nuestros resultados se basan en que los números generados sean lo bastante aleatorios. Vamos a comprobar esta afirmación haciendo estadísticas de los números obtenidos.
Comenzamos con randint , generando números enteros aleatorios, guardando la frecuencia con que aparece cada resultado, y mostrando las frecuencias en un gráfico de barras.
sage: L = 10
sage: T = 1000
sage: frecuencias = [0]*L
sage: for j in range(T):
... k = randint(0,L-1)
... frecuencias[k] += 1
sage: #Mediante ymin=0, indicamos que muestre las graficas
sage: #partiendo desde el eje de las x
sage: #(prueba a quitarlo y veras que pasa)
sage: bar_chart(frecuencias,width=1).show(ymin=0)
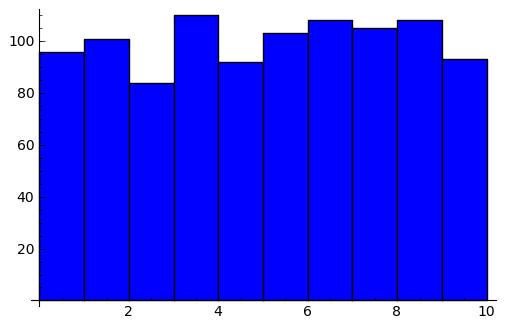
Para comprobar random, nos limitamos a separar los números entre 0 y 1 en L subintervalos distintos, y luego comprobar que en cada caja tenemos aproximadamente 1/L números. No tenemos teoría suficiente para hacer tests más sofisticados.
sage: L = 10
sage: T = 1000
sage: frecuencias = [0]*L
sage: for j in range(T):
... a = random()
... k = floor(a*L)
... frecuencias[k] += 1
sage: #Mediante ymin=0, indicamos que muestre las graficas
sage: #partiendo desde el eje de las x
sage: #(prueba a quitarlo y veras que pasa)
sage: bar_chart(frecuencias,width=1).show(ymin=0)
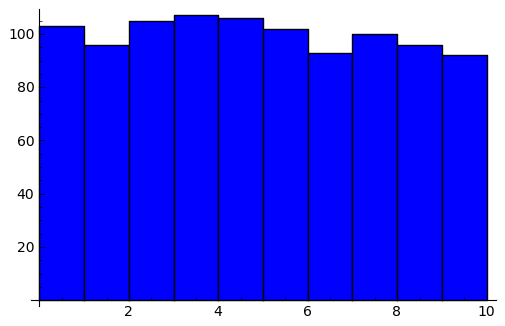
En realidad, los números generados con randint y random son pseudo-aleatorios: son aleatorios a efectos prácticos pero están generados de manera casi determinista: primero se escoge una semilla , y a partir de ahí se usa una función de apariencia aleatoria para obtener el siguiente número aleatorio a partir del anterior.
Más detalles (en inglés) en:
http://docs.python.org/library/random.html
Si fijamos la semilla, todos los cálculos posteriores con numeros aleatorios generan los mismos números, aunque lo ejecutemos en distintos momentos o en distintos ordenadores. Esto es importante para reproducir exactamente un cálculo con números aleatorios.
sage: #Fijamos la semilla para generar números aleatorios
sage: set_random_seed(123)
sage: print random()
sage: print random()
sage: print random()
sage: print randint(1,10)
sage: print randint(1,10)
sage: print randint(1,10)
0.220001316661
0.778780038062
0.0648345056353
8
2
1