Continuamos la sesión de álgebra lineal con varias aplicaciones a formas bilineales y productos escalares. Vamos a representar una forma bilineal por la matriz simétrica que la define. Por simplicidad, fijaremos el espacio vectorial y la forma bilineal como variables globales mientras sea conveniente.
¿Cuándo es una matriz simétrica definida positiva? Sabemos que una matriz simétrica es diagonalizable. La matriz es definida positiva sii todos sus autovalores son positivos.
sage: def es_definida_positiva(M):
... if not M.is_symmetric():
... raise ValueError, "La matriz no es simetrica"
... return all(l>0 for l in M.eigenvalues())
sage: B = matrix(QQ,3,3,[1,0,1, 0,2,0, 1,0,3])
sage: show(B)
sage: print es_definida_positiva(B)
sage: B = matrix(QQ,3,3,[1,0,1, 0,2,0, 1,0,-3])
sage: show(B)
sage: print es_definida_positiva(B)
True
False
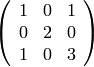
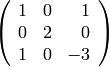
- Escribe una función que haga el mismo papel, pero usando el criterio de Sylvester ( una matriz es definida positiva sii los determinantes de sus menores principales son positivos).
- Escribe una función análoga para matrices definidas negativas.
- Usa el método random_matrix para generar 100 matrices con las que comprobar que ambos métodos dan el mismo resultado. (observación: random_matrix genera matrices no necesariamente simétricas, pero hay un truco canónico para obtener una matriz simétrica a partir de una matriz arbitraria).
Como sabemos de las clases de álgebra lineal, es fácil trabajar con un producto escalar distinto del habitual reemplazando los productos escalares por los productos escalares con la matriz B.
sage: #globales
sage: V = VectorSpace(QQ,3)
sage: B = matrix(QQ,3,3,[1,0,1, 0,2,0, 1,0,3])
Implementa los dos métodos siguientes:
sage: def son_ortogonales(W1, W2):
... '''Comprueba si los dos subespacios de V
... que se pasan como argumentos son ortogonales
... '''
... return ...
sage: def complemento_ortogonal(W):
... '''Devuelve el complemento ortogonal en V del subespacio
... que se pasa como argumento
... '''
... return ...
sage: W = V.subspace(list(random_matrix(QQ,2,3)))
sage: L = complemento_ortogonal(W)
sage: print son_ortogonales(L,W) #Deberia ser True
sage: W = V.subspace(list(random_matrix(QQ,1,3)))
sage: L = complemento_ortogonal(W)
sage: print son_ortogonales(L,W) #Deberia ser True
Fijamos el espacio vectorial V y el producto escalar B.
sage: V = VectorSpace(QQ,3)
sage: B = matrix(QQ,3,3,[1,0,1, 0,2,0, 1,0,3])
sage: base = V.basis()
sage: print base
[
(1, 0, 0),
(0, 1, 0),
(0, 0, 1)
]
- Escribe una función que compruebe si una base dada es ortogonal.
- Lo mismo de antes, pero para una base ortonormal.
El método de Gram-Schmidt permite obtener una base ortonormal a partir de una base arbitraria.
Comenzamos con una lista vacía que contendrá en todo momento un sistema ortonormal. Para cada vector de la base original, repetimos los pasos siguientes:
- Resta a ese vector su componente en cada uno de los vectores del sistema ortonormal.
- Divide el resultado por su norma para obtener un vector unitario.
- Añáde el resultado al sistema ortonormal.
sage: def gram_schmidt(base):
... base_gm = []
... for u in base:
... w = u - sum((u*B*v)*v for v in base_gm)
... base_gm.append( w/sqrt(w*B*w) )
... return base_gm
sage: B = matrix(QQ,3,3,[1,-1,1, -1,2,0, 1,0,3])
sage: gm = gram_schmidt(base)
sage: gm
[(1, 0, 0), (1, 1, 0), (-2, -1, 1)]
Verifica que el resultado es una base ortonormal, para 100 bases generadas aleatoriamente usando random_matrix .
- Escribe una función que acepte como argumentos un vector y un subespacio, y devuelva la proyección ortogonal del vector en el subespacio (usando el producto escalar B definido globalmente).
- Reescribe el método de Gram-Schmidt usando esta función.
Una matriz simétrica definida positiva representa un producto escalar. Como hemos visto, podemos encontrar una base ortonormal para ese producto escalar.
Si tenemos dos productos escalares, podemos encontrar una base que es ortonormal para el primer producto escalar y ortogonal para el segundo. El procedimiento es el siguiente:
- Encuentra una base ortonormal para el primer producto escalar.
- En esa base, el primer producto escalar tiene como matriz la identidad, y el segundo tiene una matriz B, que es simétrica.
- Gracias al teorema espectral, es posible encontrar una matriz ortonormal tal que B es diagonal. En otras palabras, existe una base ortonormal para el primer producto escalar en la que la matriz del segundo producto escalar es diagonal. Es decir, que esa base también es ortogonal para el segundo producto escalar.
Encuentra una base ortonormal para el producto escalar B1 y ortogonal para el producto escalar B2.
sage: B1 = matrix(RDF,3,3,[1,0,1, 0,2,0, 1,0,3])
sage: B2 = matrix(RDF,3,3,[3,-1,1, -1,2,0, 1,0,1])