En esta sección vamos a estudiar algunas formas de medir la eficiencia de nuestros programas en Sage, y a estudiar la complejidad de las operaciones usuales en Sage.
Medir de forma precisa este tiempo no es una tarea trivial, y los resultados pueden variar sensiblemente de un ordenador a otro. La cantidad de factores que pueden influir en el tiempo de ejecución es muy larga:
- algoritmo usado
- sistema operativo
- velocidad del procesador, número de procesadores y conjunto de instrucciones que entiende
- cantidad de memoria RAM, y caché, y velocidad de cada una
- coprocesador matemático, GPU
- ...
Incluso en la misma máquina, el mismo algoritmo tarda algunas veces mucho más tiempo en dar el resultado que otras, debido a factores como el tiempo que consumen las otras aplicaciones que se están ejecutando, o si hay suficiente memoria RAM en el momento de ejecutar el programa.
Nuestro objetivo es comparar sólo los algoritmos , intentando sacar conclusiones independientes de la máquina.
Un mismo algoritmo se puede llamar con distintos datos de entrada. Nuestro objetivo es estudiar el tiempo de ejecución como función del “tamaño” de los datos de entrada . Para ello usamos dos técnicas:
- Medir tiempos de ejecución de los programas con datos de entrada de distintos tamaños
- Contar el número de operaciones que realiza el programa
Comenzamos por medir el tiempo de ejecución de algunos algoritmos de forma empírica. Probando dos algoritmos que calculan el mismo objeto con datos de distinto tamaño nos haremos una idea de qué algoritmo es mejor para datos grandes.
Para evitar que el resultado tenga en cuenta el efecto de los otros programas que se están ejecutando en nuestro ordenador en ese mismo momento, SAGE utiliza los conceptos de CPU time y Wall time , que son los tiempos que el ordenador dedica exclusivamente a nuestro programa.
El CPU time es el tiempo de CPU que se ha dedicado a nuestro cálculo, y el Wall time el tiempo de reloj entre el comienzo y el final del cálculo. Ambas mediciones son susceptibles a variaciones imprevisibles.
La forma más sencilla de obtener los tiempos de ejecución de un comando es anteponer la palabra time al comando.
sage: time is_prime(factorial(500)+1)
False
Time: CPU 0.09 s, Wall: 0.09 s
sage: #Para datos de mayor tamanyo, tarda mas tiempo (en general)
sage: time is_prime(factorial(1000)+1)
False
Time: CPU 0.72 s, Wall: 0.76 s
Para medir tiempos más breves, podemos usar la funcion timeit .
sage: timeit('is_prime(1000000000039)')
625 loops, best of 3: 7.3 µs per loop
Para hacernos una idea del tiempo que tarda en terminar un programa en función del tamaño de los datos de entrada, vamos a hacer gráficas: en el eje x , el tamaño de los datos de entrada; en el eje y, el tiempo total.
El comando time no es lo bastante flexible, y necesitaremos las funciones cputime y walltime . cputime es una suerte de taxímetro : es un contador que avanza según hacemos cálculos, y avanza tantos segundos como la CPU dedica a Sage. walltime es un reloj convencional, pero medido en segundos desde el 1 de enero de 1970 (es el unix clock). Para obtener el tiempo dedicado a nuestro programa, tomamos los tiempos antes y después de la ejecución, y calculamos la diferencia.
sage: #cputime solo avanza cuando la cpu corre
sage: #(es un taximetro de la cpu)
sage: #Ejecuta esta funcion varias veces para ver como aumenta el tiempo
sage: #Si quieres, ejecuta comandos entre medias
sage: cputime()
2.0600000000000001
sage: #walltime avanza inexorable (es un reloj normal y corriente)
sage: walltime()
1298369972.163182
El siguiente código guarda en una lista los cpu times empleados en ejecutar la función factorial con datos de distinto tamaño.
sage: numeros = [2^j for j in range(8,20)]
sage: tiempos = []
sage: for numero in numeros:
... tcpu0 = cputime()
... 11 = factorial(numero)
... tiempos.append(cputime()-tcpu0)
Dibujamos la gráfica tiempo de ejecución vs tamaño de los datos.
sage: p1 = line(zip(numeros,tiempos))
sage: p1.show()
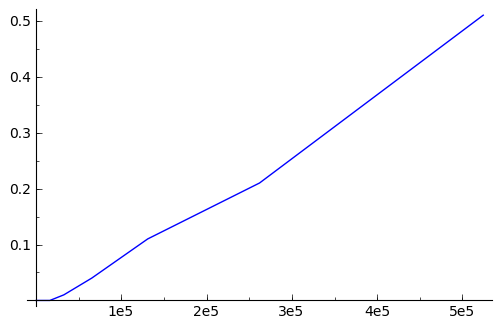
Una alternativa a medir el tiempo que tarda un programa que implementa un algoritmo es contar directamente el número de operaciones que hace ese algoritmo cuando lo ejecutamos. Como este es un tema que estáis estudiando a fondo en otra asignatura, no entraremos en detalle, pero repasamos las nociones básicas para fijar la terminología:
Definición. Dada una función g , diremos que otra función f es O(g) (y escribiremos 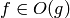 o incluso
o incluso 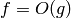 !), si
!), si 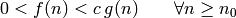 , para constantes positivas
, para constantes positivas 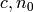 .
.
También diremos que f está dominada por g si 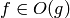 . Por ejemplo,
. Por ejemplo,
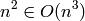
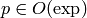
Donde 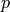 es un polinomio cualquiera y
es un polinomio cualquiera y 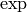 es la función exponencial.
es la función exponencial.
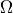 y
y 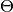 ¶
¶Así como 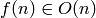 sirve para expresar una cota superior a la función f,
sirve para expresar una cota superior a la función f, 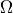 y
y 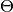 sirven para expresar una cota inferior, y una cota ajustada, respectivamente:
sirven para expresar una cota inferior, y una cota ajustada, respectivamente:
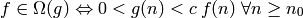
para dos constantes positivas 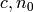 .
.
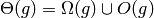
En el caso anterior, es fácil ver que de hecho 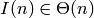 .
.
Definición . Decimos que un algoritmo tiene complejidad ó coste en O(f) (resp 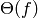 ,
, 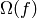 ) si su número de operaciones (como función del tamaño de los datos de entrada) es una función que pertenece a O(f) (resp
) si su número de operaciones (como función del tamaño de los datos de entrada) es una función que pertenece a O(f) (resp 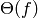 ,
, 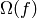 ).
).
Nota: Un algoritmo termina en una cantidad fija de operaciones, independientemente de los datos de entrada, si y sólo si tiene complejidad en 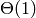 .
.
Aunque la notación de complejidad es conveniente, no deja de ser una simplificación: el número de operaciones no depende sólo del tamaño de los datos de entrada.
El coste en el peor caso es el máximo número de operaciones para un dato de entrada que tenga tamaño n.
El coste promedio es el promedio del número de operaciones sobre todos los posibles datos de entrada de tamaño n.
Las listas nos permiten almacenar una cantidad arbitraria de valores de cualquier tipo. A lo largo del programa, podemos añadir elementos a la lista, eliminarlos y acceder a cualquiera de los elementos.
Internamente, una lista es un espacio de direcciones de memoria consecutivas que contienen referencias a los objetos almacenados en la lista.
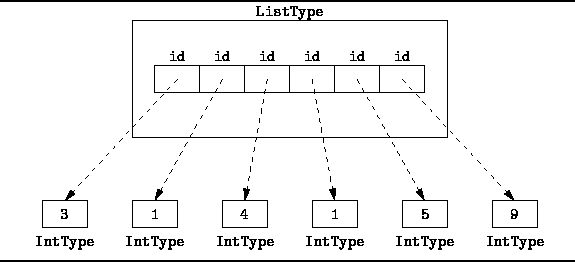
Es muy importante que las direcciones sean consecutivas. De esta forma, podemos acceder al elemento j-ésimo en poco tiempo: si la dirección de memoria del primer elemento de la lista es d , la dirección del elemento j-ésimo es d+j .
Sin embargo, mantener las direcciones consecutivas tiene un precio. Si queremos añadir otro elemento al final (usando append ), es necesario que la dirección de memoria al final de la lista esté desocupada. Si no lo está, tenemos que desplazar la lista a un nuevo emplazamiento en la memoria donde haya sitio para todos los elementos. Las listas de python reservan parte del espacio detrás de la lista, de modo que no haya que recolocar la lista demasiadas veces. Añadir un elemento en cualquier posición distinta de la última obliga a desplazar los elementos posteriores de la lista para hacer hueco al nuevo elemento.
Eliminar un elemento también puede ser una operación costosa, porque después de quitar un elemento, tenemos que desplazar el resto de los elementos a la izquierda hasta tapar el hueco que deja el elemento que hemos sacado. Observa que al eliminar un elemento cercano al final de la lista sólo es necesario recolocar una pequeña parte de la lista.
Comparamos los tiempos necesarios para eliminar todos los elementos de una lista, primero eliminando cada vez el último elemento, y después eliminando el primer elemento de la lista.
sage: %time
sage: lista=range(20000)
sage: while len(lista)>0:
... del lista[-1]
CPU time: 0.03 s, Wall time: 0.03 s
sage: %time
sage: lista=range(20000)
sage: while len(lista)>0:
... del lista[0]
CPU time: 0.17 s, Wall time: 0.18 s
Ejercicio : Compara el tiempo necesario para añadir 20000 elementos al principio y al final de una lista. Para ello tienes que encontrar un método que te permita insertar un elemento al principio de la lista, usando la ayuda.
Al añadir un elemento al final de la lista, pueden ocurrir dos cosas: que el espacio al final de la lista esté disponible, o que no lo esté. Si está disponible, sólo necesitamos O(1) operaciones. Si no lo está, tenemos que copiar la lista entera a un lugar nuevo, lo que cuesta O(n). Por tanto, la complejidad de añadir un elemento al final de una lista en el pero caso posible, es O(n).
Para evitar caer en el segundo caso con demasiada frecuencia, el intérprete de python reserva espacio extra después de cada lista. Así, cuando nos vemos obligados a recolocar una lista de tamaño n, le buscamos un espacio de tamaño 2*n, y colocamos los elementos de la lista al principio.
Sumemos el coste de añadir n elementos uno por uno a una lista:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 1+1 | 1 | 1+2 | 1 | 1+4 | 1 | 1 | 1 | 1+8 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1+16 |
| 1+1 | 2+1 | 3+3 | 4+3 | 5+7 | 6+7 | 7+7 | 8+7 | 9+15 | 10+15 | 11+15 | 12+15 | 13+15 | 14+15 | 15+15 | 16+15 | 17+31 |
Para añadir n elementos uno por uno, necesitamos hacer O(n) operaciones para añadir los elementos, y después tenemos el coste de desplazar la lista a la nueva posición. Este coste es igual a la longitud de la lista en el momento en que se tiene que desplazar. La lista se desplaza cuando añadimos un elemento a una lista de longitud 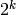 , luego es igual a:
, luego es igual a:
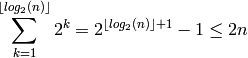
Decimos que añadir un elemento a una lista tiene coste amortizado O(1) , porque añadir n elementos siempre tiene complejidad en O(n) .
Insertar un elemento en la posición k-ésima de una lista de n elementos obliga a desplazar los n-k últimos elementos para abrir hueco. Por ejemplo, crear una lista de n elementos insertando los elementos al principio tiene coste: 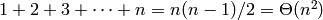
Quitar un elemento del final de la lista tiene coste O(1) (en el peor caso, no es necesario hablar de coste amortizado). Quitar el elemento en la posición k-ésima de una lista de n elementos tiene coste 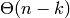 .
.
Acceder o actualizar elementos en posiciones arbitrarias no requiere recorrer la lista ni desplazar porciones de la lista, y llevan tiempo O(1) .
Si una tabla está bastante llena de elementos, es necesario ampliarla. Al igual que en el caso de las listas, es tarea del intérprete de python decidir el mejor momento para ampliar la tabla, y no necesitamos preocuparnos demasiado porque ocurre con relativamente poca frecuencia.
Las búsquedas por el hash son relativamente rápidas, aunque no lo es tanto como el acceso directo al elemento i-ésimo de una lista. Sin embargo, es mucho más rápido añadir y quitar elementos de un conjunto o diccionario que de una lista y es mucho más rápido comprobar si un objeto ya está en la tabla.
En resumen, a pesar de su uso similar, las listas son muy distintas de los diccionarios, y el coste de las operaciones elementales es distinto:
- Acceder a un elemento de un diccionario (dic[clave]) es más lento que a un elemento de una lista (lista[indice]). Sin embargo, ambos son similares. A efectos prácticos, podemos asumir que el número de operaciones es independiente del tamaño de los datos de entrada en ambos casos.
- Insertar o quitar un elemento del final de una lista es más rápido que hacerlo de un diccionario. Sin embargo, ambos son similares. A efectos prácticos, podemos asumir que el número de operaciones es independiente del tamaño de los datos de entrada en ambos casos.
- Sin embargo, insertar o quitar un elemento cualquiera de una lista es mucho más lento que hacerlo de un diccionario. Insertar un elemento al principio de una lista obliga a recolocar la lista, lo que requiere un tiempo proporcional al tamaño de la lista (en otras palabras, O(n) ).
- Comprobar si un valor está en una lista requiere recorrer toda la lista y es mucho más lento que hacer la comprobación en un conjunto o diccionario. Como tenemos que comprobar si cada elemento de la lista es igual al valor, el número de operaciones requiere un tiempo proporcional al tamaño de la lista (en otras palabras, O(n) ).
sage: lista = [k^2 for k in range(10000)]
sage: conjunto=set(lista)
sage: %time
sage: for j in range(10000):
... b = (j in lista)
CPU time: 1.70 s, Wall time: 1.71 s
sage: %time
sage: for j in range(10000):
... b = (j in conjunto)
CPU time: 0.00 s, Wall time: 0.00 s
Ejercicio : comprueba empíricamente las demás afirmaciones de arriba sobre la eficiencia de diccionarios y listas.
A modo de ejemplo, comparamos dos formas de construir una lista que tenga sólo los elementos comunes a dos listas dadas. La primera de ellos usa listas, la segunda sigue el mismo enfoque, pero con conjuntos, y la tercera usa la intersección de conjuntos (el operador & ).
sage: def interseca1(l1,l2):
... return [elemento for elemento in l1 if elemento in l2]
sage: def interseca2(l1,l2):
... #Solo necesitamos convertir l2 en conjunto, porque
... #comprobamos si los elementos de l1 pertenecen a l2 o no
... c2 = set(l2)
... return [elemento for elemento in l1 if elemento in c2]
sage: def interseca3(l1,l2):
... c1 = set(l1)
... c2 = set(l2)
... ci = c1 & c2
... return list(ci)
La segunda implementación tiene que crear un conjunto con los elementos de la segunda lista, pero después la operación de comprobación de pertenencia (in) es más eficiente.
La tercera implementación tiene que crear conjuntos con los elementos de la cada lista, y convertir el resultado final a un conjunto, pero a cambio podemos hacer directamente la intersección de conjuntos, que es más eficiente.
sage: numero = 1000
sage: #Tomamos los numeros aleatorios entre 1 y 10*numero para
sage: #que los numeros esten lo bastante espaciados, y no sea
sage: #probable que un elemento cualquiera de l1 este en l2
sage: l1 = [randint(1,10*numero) for k in range(numero)]
sage: l2 = [randint(1,10*numero) for k in range(numero)]
sage: time li = interseca1(l1, l2)
sage: time li = interseca2(l1, l2)
sage: time li = interseca3(l1, l2)
Time: CPU 0.02 s, Wall: 0.02 s
Time: CPU 0.00 s, Wall: 0.00 s
Time: CPU 0.00 s, Wall: 0.00 s
Los tiempos de las versiones 2 y 3 son muy bajos y bastante similares.
Ejercicio: Genera gráficas de tiempo de ejecución de interseca1 en función del tamaño de las listas.
Ejercicio : Estima la complejidad teórica del algoritmo usado en interseca1.
Nota: No merece la pena hacer gráficas del tiempo de ejecución para las funciones interseca2 y interseca3, porque los tiempos son tan bajos que sólo se ve ruido.
Vamos a hacer un problema del proyecto projecteuler :
Este sitio web tiene un montón de problemas que involucran ideas o conceptos de matemáticas y una cantidad importante de cuentas, de modo que el ordenador se hace indispensable. Nos ocupamos ahora del problema 45, que admite un planteamiento sencillo usando intersecciones de conjuntos:
http://projecteuler.net/index.php?section=problems&id=45
Se trata de encontrar 3 números que sean a la vez triangulares, pentagonales y hexagonales (contando el número 1 que lo es de forma trivial):
http://es.wikipedia.org/wiki/N%C3%BAmero_poligonal
Podemos generar números triangulares, pentagonales y hexagonales fácilmente y también es posible comprobar si un número es triangular ó pentagonal ó hexagonal.
Suponiendo que sabemos comprobar si un número es triangular en tiempo constante O(1), necesitaríamos O(N) operaciones para comprobar qué números menores que N son a la vez triangulares, pentagonales y hexagonales. Utilizando conjuntos podemos reducir el número de operaciones drásticamente.
La estrategia es la siguiente: primero generamos tres conjuntos, con los números triangulares, pentagonales y hexagonales, y luego los intersecamos. Escogemos conjuntos en vez de listas porque las intersecciones de conjuntos requieren menos operaciones.
sage: def busca_tph(cota):
... '''Busca todos los números menores que una cota que son
... a la vez triangulares, pentagonales y hexagonales
...
... Devuelve un conjunto con todos los numeros buscados
... '''
... #creamos el conjunto de numeros triangulares
... k=1
... triangulares = set()
... while k*(k+1)/2<cota:
... triangulares.add(k*(k+1)/2)
... k = k+1
... #creamos el conjunto de numeros pentagonales
... k=1
... pentagonales = set()
... while k*(3*k-1)/2<cota:
... pentagonales.add(k*(3*k-1)/2)
... k = k+1
... #creamos el conjunto de numeros hexagonales
... k=1
... hexagonales = set()
... while k*(2*k-1)<cota:
... hexagonales.add(k*(2*k-1))
... k = k+1
...
... return triangulares & pentagonales & hexagonales
sage: %time
sage: print busca_tph(1e6)
set([1, 40755])
CPU time: 0.02 s, Wall time: 0.02 s
sage: %time
sage: print busca_tph(1e8)
set([1, 40755])
CPU time: 0.13 s, Wall time: 0.13 s
Aumentando la cota, el tiempo de ejecución aumenta, lógicamente. En vez de hacer gráficas de tiempo de ejecución, vamos a reflexionar sobre el tiempo que debería tardar y la cantidad de memoria que necesita este enfoque para saber hasta dónde podemos buscar.
Tanto los números triangulares como los pentagonales y los hexagonales crecen de forma cuadrática . Por lo tanto, si fijamos una cota N, el tamaño de cada uno de los conjuntos triangulares , pentagonales y hexagonales será menor que una constante por la raíz cuadrada de N . Para construirlos, habremos dedicado a lo sumo 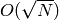 . Una vez construidos los conjuntos, la intersección de dos conjuntos de tamaño K1 y K2 se puede realizar en tiempo O(min(K1, K2)), porque basta con comprobar si cada elemento del conjunto menor está en el otro conjunto.
. Una vez construidos los conjuntos, la intersección de dos conjuntos de tamaño K1 y K2 se puede realizar en tiempo O(min(K1, K2)), porque basta con comprobar si cada elemento del conjunto menor está en el otro conjunto.
De modo que el tiempo de ejecución debería crecer como la raíz de la cota, y el uso de la memoria también, por motivos similares. Podemos permitirnos poner una cota de 1e10, y el tiempo de ejecución sólo debería aumentar unas 10 veces frente al tiempo que tardó la llamada con cota = 1e8.
sage: %time
sage: print busca_tph(1e10)
set([1, 40755, 1533776805])
CPU time: 1.49 s, Wall time: 1.49 s