|
|
|
RESUMENES
CONFERENCIANTES PLENARIOS
Angela Arenas
Polinomios asociados a subextensiones ciclotómicas y formas modulares de Hilbert
El estudio relativo a la determinación y estimación de
los coeficientes de los polinomios ciclotómicos y otros
relacionados con ellos representa un extenso capítulo de la
Teoría de Números.
El principal objetivo de esta conferencia es la exposición de
resultados sobre la determinación efectiva de los polinomios que
definen las subextensiones reales maximales de los cuerpos
ciclotómicos definidos por las raices p^n-ésimas
primitivas de la unidad, siendo p un número primo, y su aplicación
a la determinación de formas modulares de Hilbert.
Fernando Chamizo
Problemas de puntos del retículo
Ya en trabajos de Gauss y Dirichlet aparecieron problemas consistentes
en contar puntos de coordenadas enteras en ciertas regiones, y en los
últimos cien años ha habido una continua e intensa
actividad en torno a ellos. El propósito principal de esta
charla es utilizar algunas de las técnicas empleadas como
ilustración de ideas generales básicas de la
teoría analítica de números. También se
mostraran algunos resultados recientes y posibles
direcciones futuras.
Antonio Córdoba
Encuentros en la interfaz entre la Teoría de los Números y el Análisis Armónico
Las sumas trigonométricas cuyas frecuencias son los primos, o las k-potencias, tienen un gran interés en diversos problemas aritméticos y analíticos. Los lemas de restricción de las series, e integrales de Fourier, a círculos y esferas, los multiplicadores de Bochner-Riesz y la función maximal de Kakeya, el "lattice point problem" y también las sumas de Gauss, son objetos de interés en el Análisis y la Teoría de Números que exigen ir más allá de las integrales singulares de Calderón-Zygmund. En la conferencia se presentarán algunos ejemplos paradigmáticos de esta interacción que, creemos, enriquecen el conjunto tradicional de problemas aritméticos.
Luis Dieulefait
La conjetura de modularidad de Serre
La conjetura de Serre establece un vínculo entre
representaciones 2-dimensionales (impares e irreducibles) del grupo de
Galois de los racionales a valores en un cuerpo finito y las formas
modulares. En particular, entre sus consecuencias se encuentra la
"Conjetura de Taniyama-Shimura generalizada", que generaliza la
clásica conjetura de Taniyama y Shimura y predice la modularidad
de variedades abelianas de dimensión arbitraria con
"muchas" multiplicaciones reales. Más generalmente, implica la
modularidad de motivos de rango dos sobre los racionales, como por
ejemplo de variedades de Calabi-Yau rígidas (en este
último caso, la modularidad ya había sido probada por D.
y Manoharmayum en 2003).
En esta charla comentaremos en primer lugar los resultados
fundamentales de Ribet, Mazur, Edixhoven y otros que permitieron
establecer la equivalencia entre las versiones "fuerte" y
"débil" de la conjetura de Serre, resultados que combinados con
los revolucionarias técnicas de "levantamiento modular" de Wiles
y Taylor-Wiles permitieron a Wiles la demostración de la
conjetura de Taniyama-Shimura en el caso semiestable y del Ultimo
Teorema de Fermat (conclusión de una estrategia diseñada
por Frey y llevada a cabo principalmente por Serre, Ribet y Wiles).
En segundo lugar, comentaremos resultados más recientes que
llevan a una demostración de la conjetura de Serre en casi la
totalidad de casos, resultados obtenidos por el conferenciante e,
independientemente, por Khare-Wintenberger, durante los años
2003-2004-2005-2006. El punto de partida de esta demostración es
un bellísimo resultado de "modularidad potencial" de Taylor.
Haciendo uso, de modo esencial y vital, de este resultado (y utilizando
técnicas de descenso de Galois, cambio de base soluble,
representaciones virtuales, bajada de nivel para formas modulares de
Hilbert, comparación de anillos de deformación
universales bajo cambios de base, resultados de Boeckle sobre estos
anillos, etc) estos tres autores logran demostrar dos importantes
sub-conjeturas, que son las de "existencia de familias"
(Dieulefait/Wintenberger) y de "cotas superiores para anillos de
deformación y existencia de levantamientos minimales"
(Dieulefait/Khare).
Combinando estos dos resultados y resultados de tipo Wiles de
"levantamiento modular", la idea revolucionaria de Dieulefait y
Wintenberger es efectuar un "cambio de primo" para reducir la
demostración a otro caso "más sencillo" ya probado,
tomando como "punto de arranque" un caso muy específico resuelto
por Tate y Serre a comienzos de los 70 (p=3, k=2, N=1) . Este
método ya en 2003 y 2004 permite la demostración de las
conjeturas de modularidad de Fontaine-Mazur y Serre en casos de poca
ramificación. A partir de aquí, durante 2005 y 2006,
prosiguiendo con este método de "propagación" de la
modularidad (una suerte de inducción), que en cualquier caso es
sólo posible (e incluso imaginable) gracias a los dos resultados
previos que permiten efectuar el "cambio de primo", incorporando (cada
vez más) nuevos resultados tipo Wiles de Kisin y una ingeniosa
técnica de "reducción de peso" de Khare, los mismos tres
autores establecieron casi la totalidad de casos de la conjetura de
Serre (actualmente la única restricción es que el nivel
sea impar, pero Kisin ha anunciado nuevos resultados que permiten en
principio demostrar también los casos restantes).
Andrew Granville
The anatomy of integers and permutations
At first sight integers and permutations seem to be very
different, but as we look a little more closely we find some surprising
co-incidences. We will discuss these co-incidences in this talk.
Jaime Gutiérrez
Retículas en Algorítmica y Criptología
De todos es conocido que nuestro mundo físico no es lineal.
Muchos fenómenos, sin embargo, a menudo son
”linealizados” porque sólo entonces una maquinaria
matemática que trabaja razonablemente bien puede describir estos
fenómenos y producir resultados significativos.
Las retículas o retículos (lattices) son objetos
geométricos que han sido utilizados para solucionar muchos
problemas en matemáticas e informática.
Las estrategias de reducción de retículas o las denominadas LLL-técnicas son
intrínsecamente lineales. La idea general de esta técnica
consiste en traducir nuestro problema no lineal a encontrar un vector
corto en una apropiada retícula construida a partir de los datos
de entrada. Entonces, el problema del vector más corto (Shortest
Vector Problem) y el problema del vector más cercano (Closest
Vector Problem) en teoría de retículas juegan un papel
principal. En años recientes, esta técnica ha sido usada
repetidamente en algorítmica, en la teoría de la
codificación y en criptología. En esta charla la
aplicamos para :
- buscar raíces pequeñas de
polinomios multivariados con coeficientes números enteros y
atacar ciertos criptosistemas,
- factorizar números enteros en el RSA,
- computar subcuerpos en extensiones algebraicas,
- predecir números pseudoaleatorios sobre curvas elípticas,
- analizar los grafos de Cayley: bases de Groebner y bases LLL-reducidas.
Florian Luca
Propiedades aritméticas de números combinatorios
Muchas de las sucesiones de enteros que aparecen en la
combinatoria enumerativa cumplen recurencias lineales de algún
orden k con coeficientes polinomiales. En esta charla haremos
una incursión en las propiedades aritméticas de estos
números. Por ejemplo, ¿cuántos números de Stirling S(n,k)
son potencias perfectas? ¿cuántos dígitos distintos de
cero tienen los números de Catalan en sus representaciones
decimales? ¿cuántos enteros hay tales que [n!e] es un
cuadrado perfecto? ¿cuantos factores primos tienen los números
de Apéry? Mencionaremos varios resultados acerca de estas
preguntas y otras similares, así como varios problemas
abiertos.
Oriol Serra
Sobre la conjetura de Erdös-Turán para bases aditivas
Un conjunto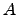 
de enteros positivos es una base aditiva de orden
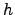para
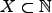si cualquier elemento de 
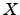se
puede escribir como suma de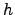
elementos de
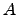, y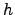
es el menor
entero con esta propiedad. Por ejemplo, un conocido teorema de
Lagrange establece que los cuadrados forman una base aditiva de
orden cuatro de los enteros positivos, y la conjetura de Goldbach
establece que los primos forman una base de orden dos para los
números pares mayores que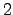 
.
La función de representación
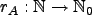de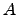
cuenta, para cada entero positivo 
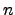, el
número de pares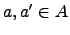 
tales que 
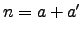. Una célebre
conjetura formulada por Erdos y Turán en 1942, todavía
sin resolver, afirma que la función de representación de una
base aditiva de
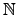no puede ser acotada. En contraste,
para cualquier función arbitraria
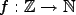, existe un conjunto
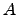
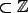cuya función de representación es 
.
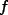Nešetril y Rödl dieron en 1985 una demostración simple
para la versión multiplicativa de la conjetura de
Erdos-Turán usando el teorema de Ramsey. Presentaremos un
argumento análogo para la conjetura original de Erdos-Turán
que da condiciones suficientes para su veracidad y en particular se
aplica a todas las construcciones de bases aditivas que se
encuentran en la literatura. Discutiremos cuestiones próximas
que pueden explicar la complejidad de la conjetura original, y
distintas de sus versiones para semigrupos abelianos en las que la
conjetura se puede o bien confirmar o bien refutar.
PONENCIAS
Francesc Bars
La ley de reciprocidad de Wiles para módulos de Drinfeld de rango 1
Maria Ángeles Gómez-Molleda
Grupos de Galois exactamente k-transitivos
Josep Gónzalez
Curvas de género 2 con multiplicación cuaterniónica y jacobiana modular
Matilde N. Lalín
Variaciones del grupo base de la Medida de Mahler
Álvaro Lozano-Robledo
Curvas elípticas de rango maximal
Juan Medina
Subgrupos de torsión de curvas elípticas sobre cuerpos de números cuadráticos
Enric Nart
n-conjuntos racionales de espacios proyectivos sobre cuerpos finitos
Ariel Pacetti
Correspondencia de Shimura en Nivel p^2
Amílcar J. Pérez A.
Avances en la D-equivalencia sobre una variedad algebraica de género 4
Jordi Pujolàs
Bisección en el 2-subgrupo de Sylow de una curva de género 2 sobre un cuerpo binario
David Roberts
Una conjetura de finitud para cuerpos de números
Antonio Rojas
Momentos de funciones Zeta de hipersuperficies de Calabi-Yau
Victor Rotger
Grafos, formas modulares e integración de distribuciones p-ádicas
Manuel Silva
Avoiding structure inside odd arithmetic progressions
Anitha Srinivasan
La Conjetura de Markoff
Juan Tena
Isogenias de curvas elípticas y formas cuadráticas binarias
Juan L. Varona
Fórmulas de inversión de Möbius para flujos de semigrupos aritméticos
|
|
|
