Este es el árbol genealógico del caballo Lion’s Share:
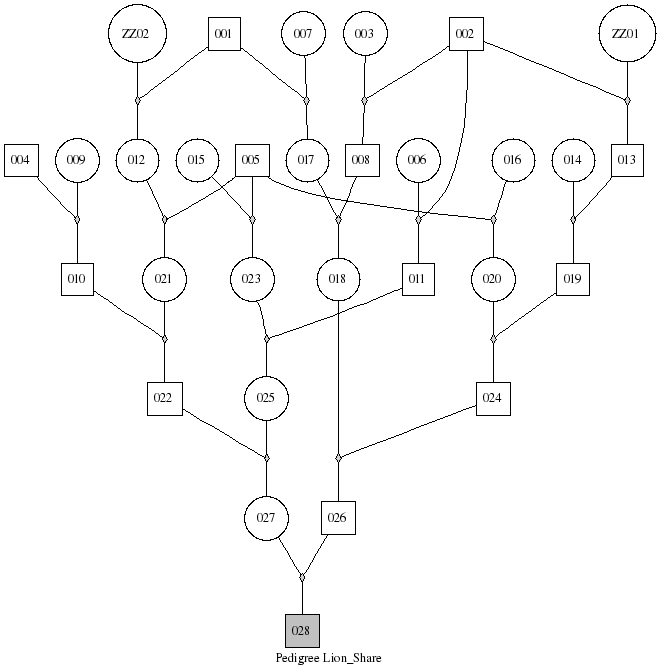
Queremos calcular la probabilidad de que los dos alelos de un gen dado provengan del mismo ascendiente, bajo las hipótesis normales de genética de Mendel. Esta probabilidad es igual a la suma, para cada ascendiente que está en el linaje tanto del padre como de la madre, del producto de la relación del ascendiente en cuestión con el padre y de su relación con la madre. La relación entre un ascendiente y su descendiente es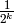 
, donde k es el número de generaciones que los separa, pero si el ascendiente aparece más de una vez en el linaje hay que sumar un término 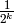por cada aparición en la generación k-ésima.
- Calcula el coeficiente de endogamia de Lion’s Share (la probabilidad definida arriba)
- ¿Qué tipo de grafo representa mejor un árbol genealógico? ¿Qué propiedades tiene?
- (opcional) Escribe un programa que acepte un grafo del tipo anterior, y el nodo raíz, y calcule la probabilidad mencionada antes. Puedes hacerlo en otro lenguaje de programación, pero en ese caso habla con el profesor antes. Un algoritmo en pseudo-código puede ser aceptable.
El grafo está sacado de: http://www.graphviz.org/content/lion_share
sage: pares = [
sage: ("025","027"), ("022","027"), ("019","024"), ("020","024"),
sage: ("027","028"), ("026","028"), ("018","026"), ("024","026"),
sage: ("011","025"), ("023","025"), ("008","018"), ("017","018"),
sage: ("010","022"), ("021","022"), ("013","019"), ("014","019"),
sage: ("015","023"), ("005","023"), ("016","020"), ("005","020"),
sage: ("012","021"), ("005","021"), ("001","012"), ("ZZ02","012"),
sage: ("003","008"), ("002","008"), ("001","017"), ("007","017"),
sage: ("009","010"), ("004","010"), ("002","011"), ("006","011"),
sage: ("002","013"), ("ZZ01","013")]
sage: ag = DiGraph()
sage: for v1, v2 in pares:
... ag.add_edge(v1,v2)
sage: attach(DATA + 'graphviz.sage')
sage: graphviz(ag, 'dot', False)
- Encuentra el recorrido de longitud más corta que pasa una vez por cada arista, para el problema de recogida de basuras.
- ¿Cuáles de entre las secuencias siguientes podrían formar parte de un truco de malabares (con las hipótesis habituales)?
- ...333334...
- ...333332...
- ...13425350...
- ...13525350...
- Completa estas secuencias de malabares hasta engancharlas con la secuencia 3333...
- ...515151
- ...525145
(opcional) ¿Cuántos circuitos hamiltonianos tiene el grafo_malabar_con_cabeza(3,4)?
Escribe el grafo de malabares con dos pelotas de un color y una tercera de otro color y altura máxima 4. Si la tercera pelota es una manzana, identifica los estados en los que puedes pegarle un mordisco.
Pepito está aprendiendo a hacer malabares con cuchillos. Se ve capaz de lanzar y recibir los cuchillos a altura 5 pero no quiere lanzar dos cuchillos seguidos tan alto por si se hace un lío al recogerlos. Modifica el grafo de tres objetos y altura 5 para evitar lanzar dos objetos a altura 5 seguidos.
- Al hablar de páginas web mencionamos un motivo por el que una cadena de Markov podría converger a una u otra distribución de probabilidad dependiendo del punto de partida. Muestra un grafo concreto que tenga este problema.
- Estudia el problema de la convergencia en el circuito con dos vértices, que te mostramos abajo: ¿converge la distribución de probabilidad de los caminos aleatorios que comienzan en el vértice 0? ¿y en el vértice 1? ¿se aplica tu razonamiento a todos los circuitos de cualquier longitud (grafos con vértices 0,1,..,n tales que 0 está unido a 1, 1 a 2, ..., y n a 0)?
.
.
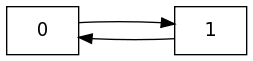
- Encuentra otro grafo fuertemente conexo, y que no sea un circuito, pero tal que la distribución de probabilidad no converja desde algún punto de partida.
- Busca en la literatura (o en internet, pero llegando a una fuente de confianza), las hipótesis bajo las cuales la distribución de probabilidad de una cadena de Markov converge a una misma distribución de probabilidad, independientemente del punto de partida. Razona si los grafos que vimos al estudiar el problema de evolución verifican esta propiedad.